꿀잼 기계항공공학

 일반물리학에서 그 내용이 그렇게 어렵지는 않은 상대속도! 하지만 상대속도라는 개념이 역학의 여러분야에서 종종 활용되기도 합니다. 주로 ... 문제를 풀고 해석하는 쪽이지요. 

 이번 포스팅에서는 상대속도의 개념이 뭔지, 그리고 어떻게 활용되는지 한 번 깊게 고민해봐용!!

상대속도란??

 상대속도란 관측자의 관점에 따라 계산하는 속도입니다. 이렇게 계산해봅시다. 

 이런 그림을 생각해봅시다. 그럼 A가 B를 봤을 때 A는 B가 몇 m/s로 움직이고 있는 것으로 보일까요?

5m/s로 보일것입니다. 왜냐면 A는 가만히 있으니까요. 그런데 만약 A가 움직일 경우에는 B가 어떻게 보이게 될까요??

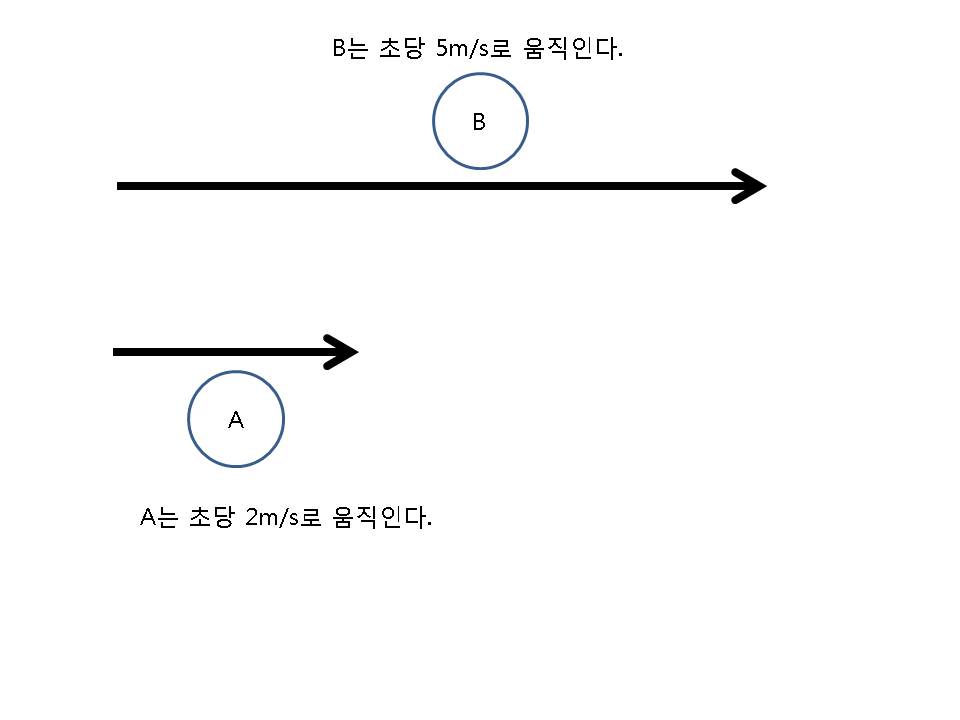
 이번에는 A가 2m/s로 움직인다고 가정해봅시다. 그럴 경우 A는 어떻게 B가 보일까요??

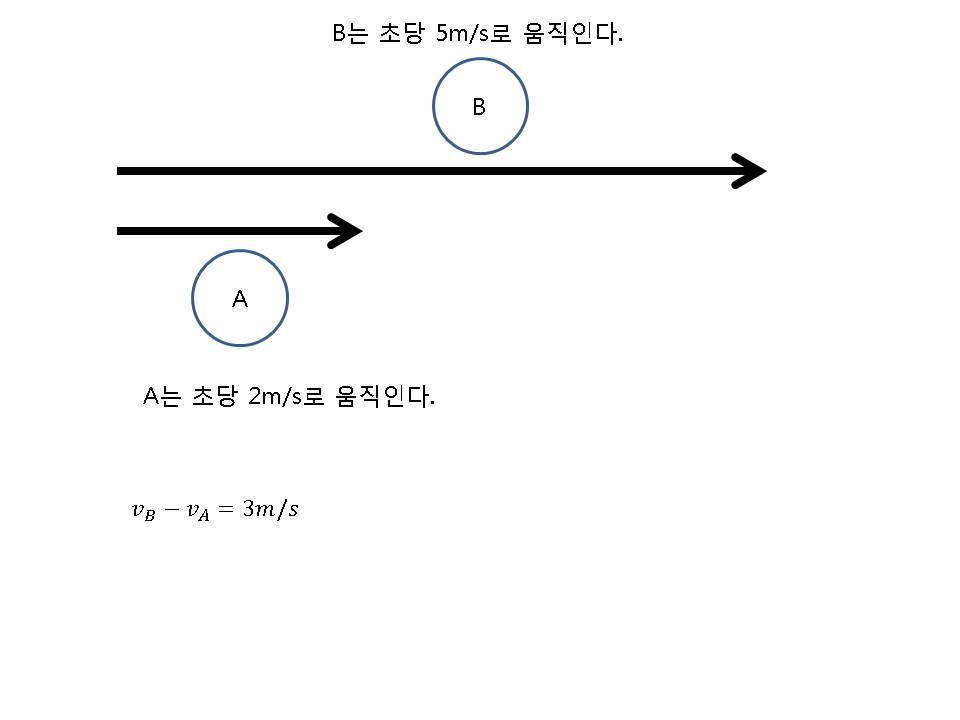
 그러면 A가 움직이고 있는 그 속도는 빼주어야 간단하게 비교할 수 있겠지요? 그럼 B에 속도에서 A의 속도만큼만 빼주면 A가 보는 B의 속도가 되겠지요.  간단히 그림으로 나타내면 다음과 같습니다. 

 위 그림은 A의 속도를 빼고 B의 속도를 바라봤을 때를 나타낸 것입니다. 즉 상대속도란 누군가를 기준으로 했을 때 관찰되는 상대방의 속도를 표현한 것이라고 볼 수 있지요. 그럼 이런 상대속도가 기계공학에서는 어떻게 활용이 될까요? 어느 역학에서 자주 사용이 될까용??

어느 분야에서 사용되는가?

 아마 기계공학에서 뽑자면 유체역학과 동역학에서 활용이 많이 되지 않을까요? 실제로 그렇습니다. 그럼 어떤식으로 이용이 될까요?

 이 그림 중 (b)의 Reflected Expansion Waves의 그림을 주목해주세요. 기체역학이라는 분야에서 쓰는 것입니다. 충격파가 벽에 반사되어 움직이면 충격파가 움직이는 속도도 고려해서 계산을 해야하는 데 그러려면 상대속도라는 개념을 활용하여야합니다. 음.. 충격파 이야기는 언젠가 때가 되면 다시 이야기해야겠네요...

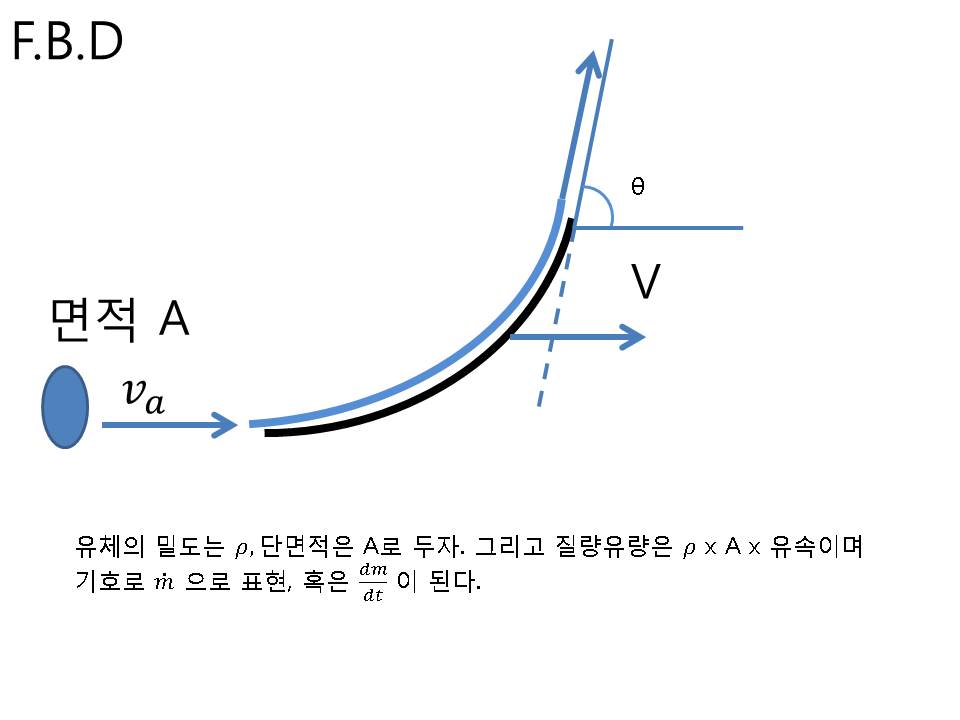
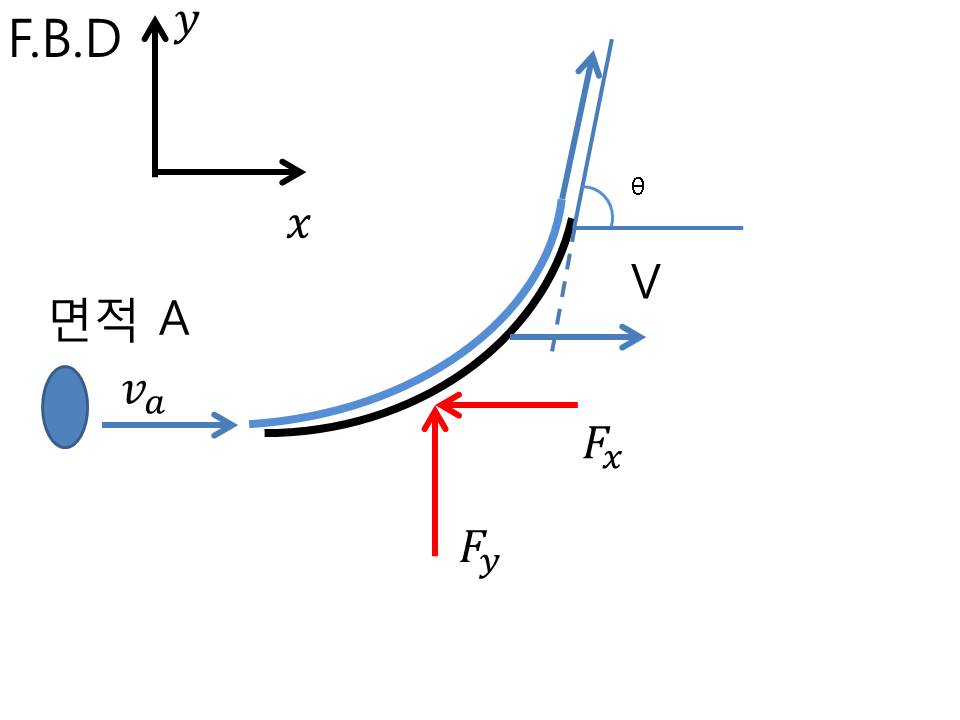
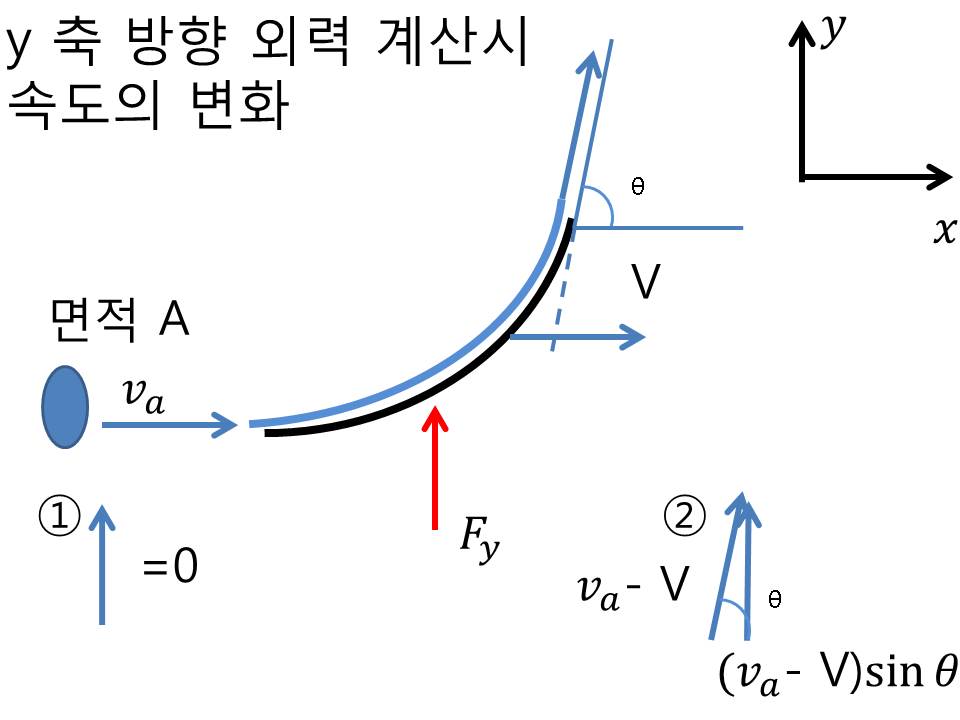
 이 문제는 밑에 바퀴 달린 물체가 V_0 이라는 속도로 움직이고, 이 물체에 부딫치는 유체가 V_1 속도로 움직이면 그 때 물체에 작용하는 수레의 힘을 구하는 것인데요. 이것은 유체 속도 이외에도 수레의 속도도 고려해야하는데요. 왜냐면 수레가 움직이게 되면서 빠지는 유량이 있기 때문이에요. 수레 속도를 같이 고려하면 헷갈릴 수 있으니 아예 수레 속도는 빼놓고 계산을 하는게 편하겠지요. 그래서 상대속도를 활용해야합니다. 

마치며...

 아직은 블로그에 쌓인 정보가 적어서 상대속도의 활용에 대해서 좀 더 자세히 설명하지 못했습니다. 기회가 되면 좀 더 보완을 해보고 싶네요. 상대속도 이외에도 다양한 개념들이 기계공학과 물리학에 있습니다. 저는 꾸준히 꾸준히 기계공학, 그리고 기사 공부를 하며 풀이를 재밌게 할 수 있다면 그렇게 해보고 싶습니다. 

 안녕하세요! 공돌이인생무상이에요. 이번 포스팅은 물리에서 상식으로 통하는 뉴턴의 제 2법칙에 대해서 상세하게 해석하고 생각해보는 포스팅을 작성해보려고 합니다. 

 뉴턴의 제 2법칙은 간단히 말하면 F=ma 라고 외우고 다니던 분들 많았지용? 그렇지만, 뉴턴의 제 2법칙 사실 그렇게 간단하게 생각할 수 있는게 아닙니다. 과연 원래는 어떻게 서술되어있었는지 한 번 볼까요?

뉴턴의 제 2법칙의 원형

 본래 형태는 뉴턴이 작성했던 책 프린시피아(Principia, 번역제목 : 자연철학의 수학적 원리)에 서술되어 있습니다. 그럼 프린시피아의 원래 서술은 이렇습니다. 

∑F = dp/dt 

이 수식은 외력의 총합은 dp/dt 즉, 운동량의 시간 변화율과 같다는 것입니다. 물리 시간에 운동량이란 mv(질량 x 속도)라고 배웠었지요. 즉... 이 식을 다시 서술하면 

∑F = d(mv)/dt 

로 다시 변환할 수 있습니다. 대부분의 물리 서적들은 그냥 F=ma라고만 간단히 말을 합니다. 자세히 서술하기엔 종이 양이 많이 나가게 되지요. 그리고 한 가지 이유가 더 있습니다.

왜 F=ma 라고만 소개하지?

 제 생각에 이걸 이해하기 위해서는 뉴턴의 운동 법칙이 어떠한 가정을 가지고 있는지 알아야 합니다. 뉴턴의 법칙에서 가정하고 있는건... 고등학교 물리 시간에 배웠을 때는 가정에 대한 이야기가 없었습니다. 하지만, 대학에선 그걸 알려주지요. 뉴턴의 법칙에 중요한 가정은... " 외력이 작용하는 물체는 질점으로 가정한다." 입니다. 질점이란게 뭔가요? 라고 물을 수 있는데요. 질점이란 것은 부피 없는 점입니다. 즉, 뉴턴의 법칙은 물체를 점으로 가정해서 운동을 서술한다는 것이지요. 고등학교나 일반물리 초반의 내용은 이 질점의 질량이 시간에 따라 변하지 않기 때문에 이 수식을 간단히 표현해도 상관이 없습니다. 우리가 일반적으로 외웠던 그 내용...

F = m(dv/dt)

라고만 말을 해도 상관은 없는 것이지요. 왜 기호 ∑는 없느냐? 외력은 하나만 작용한다고 가정하기 때문에 굳이 외력의 총합이라고 말하지 않아도 상관이 없는 것이지요. 

 앞으로 물리를 꾸준히 공부하고 더 깊게 활용해볼 생각이 있으신 분이라면 F=ma라고만 간단히 외우는 것 보다는 원본의 내용 ∑F = d(mv)/dt 로 이해하는 것을 추천드립니다. 왜냐면 이걸로 알아둬야 앞으로 활용할 유체역학, 재료역학 등 다양한 역학에서도 고민하지 않고 즉시즉시 활용할 수 있습니다.

이 내용을 어떻게 활용해보나??

 그럼 이제 이것이 어떻게 활용되는지 직접 보여주면 되겠지요.   

 아래 사진은 VECTOR MECHANICS FOR ENGINEERS DYNAMICS 10 TH 에 수록된 샘플 문제입니다. 

 이 문제가 적절해보이네요. 우리가 새로 적용할 뉴턴의 제 2법칙에 말이지요..! 이 문제는... 외력을 추적하는 것인데요. 평범한 질점이 아닌 유체일 경우에 해당합니다. 그럼... 자유물체도를 그려봐야겠네요.

위 그림들은 자유 물체도(Free Body Diagram)를 그리는 것에서 부터 시작하여 수식을 만들고 그 다음 계산을 하는  것 까지 한 것입니다. 

마치며...

 저는 이 문제를 푸는 것이 중요한 것이 아니라, 뉴턴의 제 2법칙을 잘 쓰기 위해 어떻게 이해할 것인지를 논하려고 포스팅을 한 것입니다. F=ma 식의 암기보다는, 기본적인 수식의 이해가 중요하다 생각해요. 그래서 다양하게 활용하기 위해서는 뉴턴의 2법칙의 원형을 이해하고 이를 활용하는것이 더 유익하다 이런 것입니다.

 그럼 즐거운 물리학...또 즐겁게 생각하고 고민해보자구용!!