꿀잼 기계항공공학

 안녕하세요!~ 공돌이인생무상입니다. 이번 포스팅에서는 일반기계기사문제를 풀면서 괜찮은 내용의 문제가 있어서 포스팅으로 남겨보려고 합니다.  일반기계기사 핵심예상문제집에 보니 요런 문제가 있었습니다. 

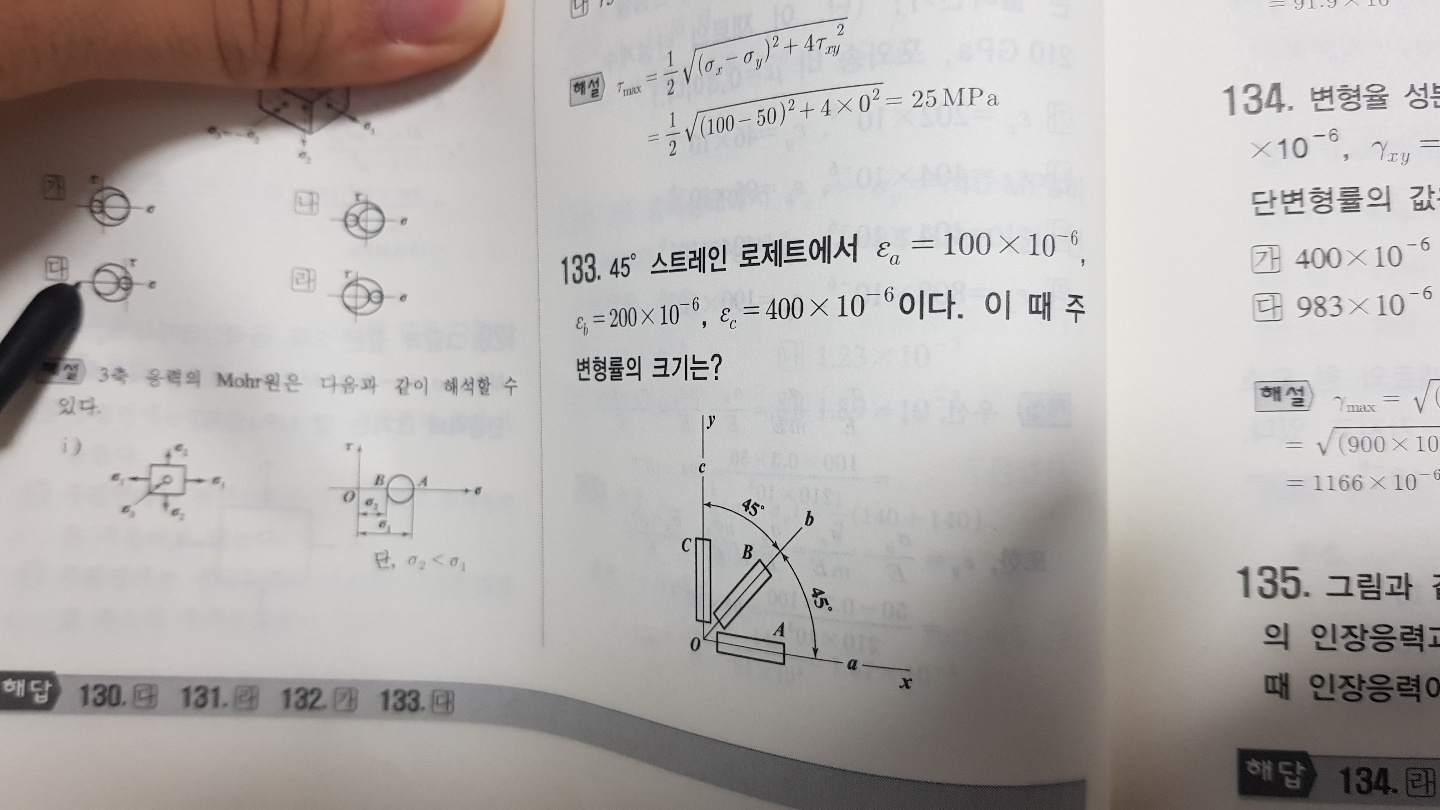
 호오.. 스트레인 로제트가 무엇이기에 이렇게 문제까지 내는것일까? 이 문제 풀이는 간단하긴하다. 그저 수식을 단순히 활용하기만 해도 잘 풀린다. 그러나 한 가지 짚고 넘어가볼만한게 있다. "스트레인 로제트".

 스트레인 로제트라는게 대체 무엇일까?

스트레인 로제트? 

  몇 몇 재료역학 서적에 보면 스트레인 게이지 (Strain gauge)라는 것을 언급한다. 이 걸로 변형률을 측정할 수 잇다고 한다. 맞다. 얘가 변형하면서 저항이 변하면 출력 신호도 변하고, 그 변화를 감지해 변형률을 측정할 수가 있다. 그건 너무 자세한 것 같고...( 추후 원리와 종류를 자세히 다뤄볼 예정) 일단은 스트레인 게이지가 어떻게 생겼는지, 로제트는 또 뭔지 알아보기만 해보자. 

 스트레인 게이지의 종류들을 나열해둔 것인데 좋은 자료인것 같아 참조해봤다. 1 element를 문제처럼 붙일 수 있지만 아니면 3element를 설치해서 계산해보는 방법도 있다. 아, 로제트라는 건 결국 스트레인 게이지를 여러개 붙인 형태를 말하는 것이다. 

 스트레인 게이지는 자세히 보면 요렇게 생겨있다. 저 검은 부분이 전류가 통하는 부분으로, 저 부분이 손상되면 측정을 할 수 없고... 그리고 이 손톱보다도 더 작은 장비는 비싸니까 잘 다뤄야한다. 엄청 비싸다. 저거 한 장에 2만원이...

본격 로제트 문제는 어떻게 접근해야하나?

 이제 문제에 본격적으로 접근해보자. 결국 3개의 방향에 설치된 스트레인 게이지의 변형량을 이용해 문제를 해결해보는 것인데... 어떻게 접근해볼까?

 이 문제는 b가 기울어져있음을 알고, 그런 다음 기울어진 면에 대한 평면응력식을 적용하는 식으로 접근하면 된다. b의 변형률은 알고 있지만, 전단변형률을 모르니까, 전단변형률을 구하기 위해서 b에 대한 변형률을 계산하는 식을 불러들이는 것이다. 

 전단변형률을 안다면 주변형률의 최대 최소값을 구하는 것은 어렵지 않은 문제이니까, 우선 전단변형률부터 얼른 구해보도록 하자.

 기울어진 면에서의 변형률을 알고, 반대로 전단 변형률을 모르는 상태이기 때문에 전에 다뤘던 변형률간의 관계식에서 기울어진 면에 대한 변형률이 아닌 전단 변형률을 구하는 식으로 활용하면 된다. 

 전단변형률 Gammar의 크기를 구했다. 이제 거의 끝났다고 보면 될 듯하다.  

 여기서도 저번에 다뤗던 수식을 통해서 풀이를 하면 된다.  

 전단변형률을 알게되니 주 응력의 최대 최소는 그저 수식을 대입만 하면 될 뿐이다. 아, 중요한 응력들을 다 알고 있으니까 주 전단변형률도 바로 계산이 가능할 것 같다. 

 이렇게 답을 구했다면, 그럼 주 전단변형률의 크기에 대해서 궁금할 수 도 있을 것 같다. 그치만 주 전단변형률의 크기는 이미 저 풀이 안에 있다. 근호 (루트) 씌어진 항이 바로 주 전단변형률의 크기인 것. 저번에 수식을 다뤄봐서 알겠지만, 주 전단변형률의 크기는 주 전단응력의 크기와 달리 1/2항이 없다는 점만 알고 있다면 실수하지 않고 맞춰낼 수 있을 것이다. 

 일반기계기사 시험을 준비하다 보면 재료역학에서 응력의 조합 상태에 관한 챕터를 만날 수 있다. 아주 어렵게도 삼각함수로 떡칠이 된 챕터인데 처음 보면 이 삼각함수 조합에 여길 어떻게 공부하고 해쳐나가야 될지 막연한 느낌이 들 법도 하다. 

 하지만 알고나면 외울 수식이 그렇게 많지가 않다는 것을 알게 될 것이다. 다만 조심할 부분이 한 두 군데 있다는 것뿐.. 그럼 어떤 수식을 외워두면 쉽게 빠르게 맞출 수 있을까 알아보도록 하자. 

수식이 어떻게 생겼을까??

 이 사진은 1축 응력일 경우 면이 기울어지는 각도에 따라 응력이 어떻게 변하는지 표현한 것이다.  으아.. 이렇게 삼각함수가 많이 있다니... 으아아아아!!! 그렇지만 이 부분은 외워두도록 하자. 기사 문제에 가끔씩 나올 것이다. 아마 재료역학 책이 있으신 분들이라면 이 부분은 책에서 따로 수식을 유도하고 증명해두었을 테니까 그 부분을 참고하셔도 좋다. 

 이 수식들은 평면응력 상태라고 해서 x, y 축에 작용하는 수직 응력과 전단응력이 작용할 때 물체 내부의 면을 기울이면 응력이 어떻게 작용하는지 표현한 수식이다. 어렵게 보이지만 사실 크게 어려운 부분이 아니다. 왜냐면 외우기 쉽게 되어 있는 부분이기 때문이다. 

 붉은 네모 친 부분은 똑같으며, 푸른 네모 친 부분은 부호만 바뀌어 있다. 또한 전단응력의 경우 앞의 빨간 네모 부분은 없어지고 대신 파란 네모 부분의 삼각함수만 바뀌어 들어가 있으니 그런 규칙성을 잘 파악해서 외워두면 쉽게 외워둘 수 있다. 

 2축응력의 경우는 평면 응력에서 전단응력에 관한 내용이 빠져있기 때문에 전단응력 항만 0으로 대입해서 외워도 되고 아니면 굳이 외워둘 필요는 없는 부분이다. 

 이 수식들은 주 응력들의 크기를 구하는 수식이다. 주 응력이란 간단히 말해서 면을 돌렸을 때 나올 수 있는 최대 응력과 최소 응력을 말하는데, 그 크기도 간단히 외워둘 수 있다. 어떻게? 

 수직 응력의 경우는 x 축 응력과 y 축 응력을 더한 것에서 반으로 나눈 것과 최대 전단응력 값을 더하면 최대 주 응력, 빼면 최소 주 응력 값이 나온다. 

 최대 전단응력 값은 주 응력 값 뒤의 루트 항인데 이 항은 Morh 원의 반지름이 된다는거 정도는 외워둬야 한다. 

변형률은 비슷한데 한 가지만 다르다.

 평면 변형률 또한 평면 응력과는 수식에서 별 차이가 없다. 다만, 전단력 관련된 항이 좀 달라졌다. 그냥 수식을 배치한 게 아닌 x 0.5가 추가되어 있으니 요 부분만 주의해서 외워둔다면 헷갈리지 않을 것이다. 

 이것은 최소 최대 주 변형률의 크기에 관한 수식이다. 역시 전단력 부분에서 0.5가 곱해진 항이 추가되어있다. 그럼 주 전단 변형률 또한 마찬가지로 적용이 되어 있음을 알 수 있을 것이다. 

 주 전단 변형률또한 마찬가지이다. 그럼 이 챕터에서 외워야 할 수식들을 간단히 정리하여보면 다음과 같다. 

단순 응력일 때 각도를 구하는 방법에 대해 물어볼 수 있으니 이 부분 암기해둘 필요가 있을 것 같다. 또한, 단순 응력 상태에서 물체 내부의 면이 기울어졌을 때 응력이 어떻게 되는지에 대해 묻는 문제도 간간히 나온다. 그 문제들을 대비해 수식 두 개 정도는 추가로 암기해두면 걱정 없을 것 같다. 결론은 혹시 모르니 여기 수식 3개 정도는 꼭 외워두고 시험장에 가보자. 

 아래쪽은 평면 응력일 경우의 응력 수식과 변형률에 대하여 서술한 수식들이다. 

 응력이 이 그림처럼 작용하고 있을 경우 물체 내부의 면이 기울어질 때 응력이 어떻게 변하는지 파악하는 수식들이 아래에 나와있다. 얘들은 어쩔 수 없다. 외워둬야한다. 

  총 3개의 수식들이 나오는데 수직응력의 경우 부호가 반대로 되어 있다. 또한 전단응력은 수직 응력의 앞 1/2(시그마 x + 시그마 y) 항만 없애고, 삼각함수를 교체시켜주면 된다. 요렇게 외워두자. 

 주 응력의 크기는 전단응력쪽만 외워두면 된다. 참고로, 최대 전단응력의 크기는 모어원의 지름이 된다는 것 기억해두자. 

 변형률 같은 경우 수식이 약간 변경되어있다. 수직 변형의 경우 부호가 교차되는 것이 아니라 아예 바뀌어 서술되어 있으며 전단 변형 또한 앞의 1/2가 빠지고 부호가 바뀌게 변경된다. 

 변형률의 경우 크기도 역시 변경되는데 전단 변형률 항에 4가 빠지게 된다. 또한 최대 전단변형률은 전단응력과 달리 앞에 1/2가 없어진다는 점 참고해야 할 것이다. 

 여기 나오는 수식들 중에서는 응력부분은 반드시 외워둬야 기계기사 준비하는데 에러 사항이 없을 것이다. 전단 변형률 부분은 그렇게 잘 나오는 부분이 아니기에 고득점을 준비하시는 분 아니라면 굳이 외워갈 필요는 없다. 꼭 외워야 될 수식이라면 단순 응력 부분에서 3개, 평면 응력 부분에서 6개 총 9개 수식만 확실하게 알아두고 외워두면 문제없을 듯하다.