반응형
안녕하세요! 공돌이 인생무상입니다!
저번에는 보 문제 중 외팔보의 단순한 단위하중에 이어서 이번에는 좀 더 어려운 하중에 대한 문제풀이를 해보고 적응해보는 시간을 가져보려고 해용!
문제의 출처는 BEER 외 2인, VECTOR MECHANICS FOR ENGINEERS 10th 에서 가지고 왔습니다.

첫 번째는 어디를 중심으로 문제풀이를 시작할 지 정하는 것입니다. 저는 A 점을 기준으로 문제풀이합니다. 이 문제같은 경우 직접해보면 왜 A 점 기준으로 문제풀이해야하는지 명확히 보입니다. B 점 기준으로 해도 되지만 그럴 경우 도심 지옥을 맛볼 것입니다...
그리고 저는 늘 언제나 오른쪽이 +x 방향이며 위쪽이 +y 방향입니다.

이 문제처럼 삼각형이나 다른 도형의 모양으로 단위하중 그래프가 그려지면 그 때부터 도심의 위치를 찾고 그 곳에 하중이 작용하는 것으로 계산해야합니다. 그렇게 해야 반력을 구할 수 있습니다. 그리고 지지점의 모멘트 또한 구할 수 있죠. 즉, 분포하중이 복잡한 모양인 경우에는 분포하중의 면적과 함께 분포 하중 그래프의 도심 위치를 정확히 찾아내지 못하면 문제 풀이가 안될 겁니다. 이것이 이전 포스팅에서 다뤘던 단순 단위하중분포와의 차이점입니다.

이렇게 수식으로 풀이하는 방법도 있겠으나, 단위하중은 단위로 표현하면 N/m 로 하중에 보의 길이를 나눈 값입니다. 즉, 1m 당 보가 받는 하중이란 말과도 같은것인데요. 공학적으로 보면 하중 단위가 되기 위해서는 보의 길이와 같이 어떤.. 길이와 관련된 수치를 곱하면 하중이 됨을 짐작해볼 수도 있습니다.

이 그림은 단위하중에서 하중으로 보를 변환한 모습입니다. 실제 보에 작용하는 하중은 wL/2 이며 하중이 작용하는 위치는 삼각형의 도심부... 즉 A점에서 x방향으로 2L/3 지점 떨어진 곳이네요.

이것은 B 지점에서의 반력과 반력 모멘트를 구한 것입니다. ㅎㅎ

이 것은 A 지점에서 x 만큼 떨어진 지점에서의 하중의 함수를 그리기 위해서 수식을 사용한 것입니다. 검은색으로만 그리면 헷갈릴 것 같아 하중은 녹색으로, 모멘트는 붉은색으로 표기했습니다.

여기에선 전단력의 선도가 나오고...
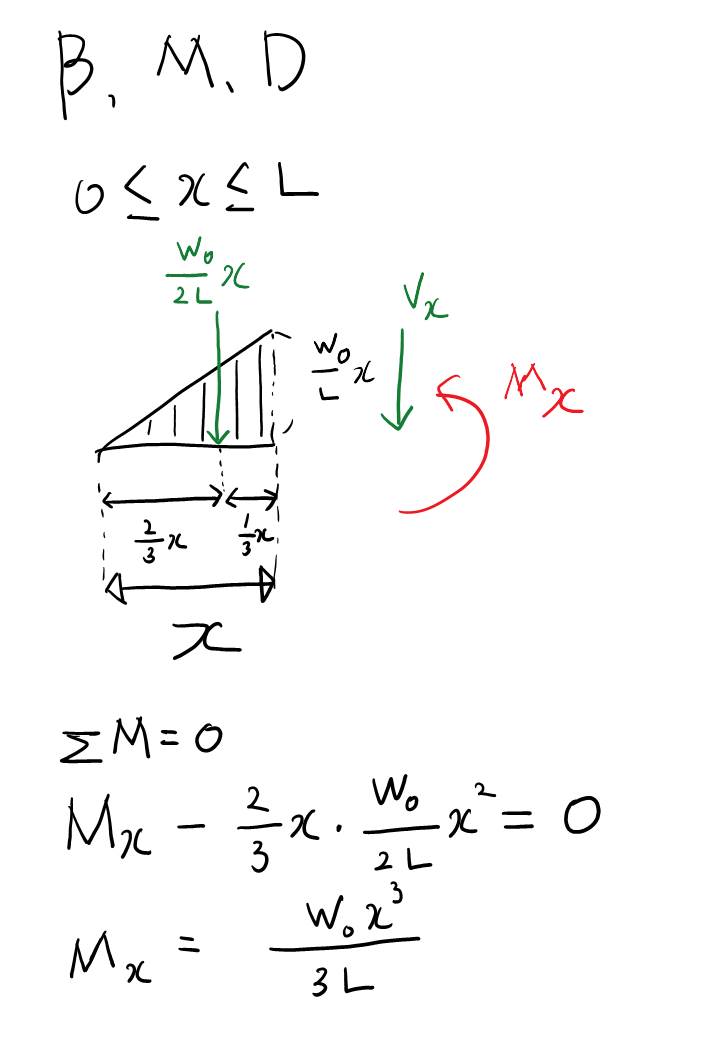

모멘트의 선도입니다. 외팔보의 경우 SFD, BMD 검산이 간단한데요. L( 보의 전체 길이) 를 넣어서 B 지점에서의 반력과 모멘트값이 나오면 풀이가 성공한 것입니다. 여기서는 삼각형만 대응했지만, 단위하중이 2차, 3차 여러 복잡한 모형으로 나와도 함수의 넓이 구할 줄 알고, 도심 구할 줄 알면 어떤 문제도 대응 가능합니다!
반응형
'기계공학- 일반기계기사 > 정역학 및 재료역학' 카테고리의 다른 글
| [정역학] Beam(보)문제 해결편 - 단순보의 집중 하중 에 대한 대응법 (3) | 2024.06.08 |
|---|---|
| [정역학] Beam(보)문제 해결편 - 정정보의 간단한 단위 하중 에 대한 대응법 (0) | 2024.04.13 |
| Beam ( 보 ) 의 해결법 - 정정보, 단순보, 간단한 하중일 경우 접근법 (0) | 2021.12.12 |
| 일반기계기사 - 트러스 구조물이 나올 경우 (간단한 문제의 경우) (0) | 2021.03.06 |
| 단면 2차 모멘트에서 파생된 계산법들을 재밌게 풀어보자 (1) | 2021.03.01 |