반응형
안녕하세요! 공돌이 인생무상입니다. 이번 포스팅에서는 저번에 포스팅했던 단면 2차 모멘트에 이어 단면 2차 모멘트와 관련있는 개념들을 한 번 알아보도록 합시다.
회전 반경
회전 반경은 주로 기둥의 좌굴에 대해 계산할 때 많이 쓰는 개념입니다. 이 회전 반경이란 것은 물리적인 의미가 있다기 보다는 평균값과 비슷한 개념이라고 보시면 됩니다.

간단하게 위의 수식처럼 계산을 하는 것인데 이게 왜 평균값과 비슷한 개념이라고 말하는 것일까요?

위의 식이 우리가 알고 있는 단면 2차 모멘트에 관한 기본 식인데요. 저 적분된 식에서 출발하지 않고 이렇게 생각해봅시다.

우리가 계산하는 물체들이 모두 균일하다고 생각했을 때 그 때 도심을 중심으로한 평균 반경은 어떻게 될 까요? 그 평균 반경을 구하는 것이 회전 반경이라는 개념으로 보시면 될 것 같네요.

그러면 간단하게 r이라는 값 (위에서는 K로 언급)을 구할 수 있게 됩니다.
어떤 물리적 의미가 아니라, 수학적으로 뭔가 평균을 구하거나 계산하기 위해 사용되는 개념이라는 것 정도로 알아둡시다. 참고로 재료 역학에서는 이런게 몇 개 뿐이지만, 유체역학에서는 몇 가지가 더 있어요. 추후에 재미있게 집필해보고 싶군요.
평행축 정리
만약 우리가 구하는 도형의 단면 2차 모멘트나 관성 모멘트를 구하여야하는데 물체의 도심이나 무게 중심에서 구하지 않고 임의의 다른 곳을 기준으로 하여 구하여야한다면 어떻게 계산해야할까요?
그래서 필요한 계산방법이 평행축 정리라고 이해하시면 됩니다. 이번에는 단면 2차 모멘트만 간단하게 살펴볼까요?

이런 상황을 가정해봅시다. 사각형의 단면 2차 모멘트와 그 도심을 구하는 것입니다. 다만 단면 2차 모멘트를 도심을 기준으로 구하는 것이 아닌 임의의 원점을 기준으로 구해봅시다.
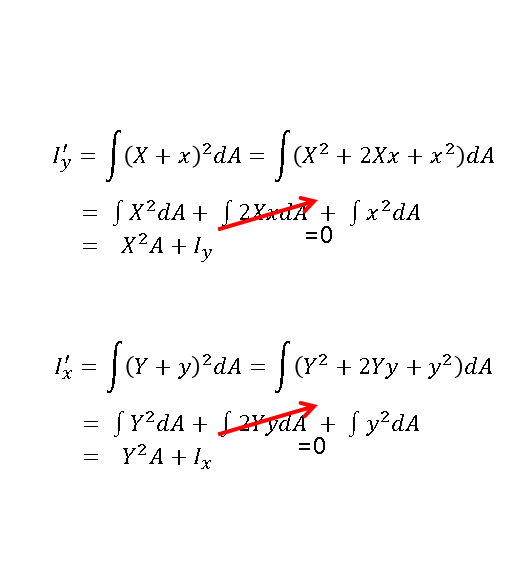
도심을 기준으로 구할 때보다 약간 다르게 수식이 변경되었습니다. 도심에서 한 변까지의 거리를 x, y로 해서 구하지 않고 도심의 좌표 X, Y가 추가가 되면서 관성모멘트를 구하는 것으로 바뀌었습니다. 적분 기호 속 괄호의 수식이야 완전 제곱식을 전개한 후 하나하나 살펴봅시다.
그러면 Ix'과 Iy' 을 구할 때 뭔가 하나 이상한 부분이 있을 겁니다.

요 두개가 왜 0이 되었을까요? 단면 1차 모멘트에서 말하지 않고 넘어간 것이 있었습니다. 만약 단면 1차 모멘트를 구할 때 x, y 가 도심을 지나갈 경우 단면 1차 모멘트는 "0" 이 됩니다. 그래서 이 항은 0이 되어 날라가게 되는 것입니다.
그렇게 되면 남게 되는 것이 다음과 같습니다.

임의의 좌표에서 단면 2차 모멘트를 구하게 된다면 도심이 임의의 원점에서 얼마나 떨어져 있는지만 알아두면 될 것입니다. 알아봤으니 한 가지만 더 해볼까요? 마찬가지로 사각형입니다.

아니 왜 똑같은 사각형인데 왼 쪽은 분모가 12이고 오른쪽은 분모가 3이 되어 있을까요? 이것도 평행축 정리를 이용하면 간단하게 해결되지요. 그럼 그 해결과정을 한 번 알아보도록 합시다.

이 수식을 써서 사각형의 밑 변을 기준으로 단면 2차 모멘트를 계산해보도록 합시다. 도심을 중심으로 하지 않았기 때문에 도심 기준의 단면 2차 모멘트랑 다른 값이 나오겠네요.

사각형의 밑변은 도심에서 h/2 만큼 떨어져 있기 때문에 이 h/2를 제곱하고 넓이를 곱한 것에 도심에서 구한 단면 2차 모멘트를 더하면 됩니다. 이렇게 평행축 정리를 활용할 수 있습니다.

이 그림에서 왼 쪽은 분모가 12가 되고 오른쪽은 3이 된 게 왼쪽은 도심을 중심으로 단면 2차 모멘트를 구한 것이고 오른쪽은 밑변을 중심으로 단면 2차 모멘트를 구하였습니다. 다만 밑변을 중심으로 하면 도심에서 h/2만큼 아래로 이동하니까 그걸 반영해 평행축 정리를 이용한 것입니다.
단면 계수
단면 계수는 또 무엇일까요? 단면 2차 모멘트는 정말 뭔가 많이 나오네요. 간단히 말하면 응력과 토크, 응력과 모멘트의 관계식을 구할 때 쓰기 위한 개념정도로 이해해두시면 됩니다.

원래 단면계수라는 개념이 비틀림 응력과 굽힘 응력을 수학적으로 유도하기 위한 과정에서 나오는 것입니다. 그치만 기계기사 시험에서는 이를 인장응력을 구하는 수식처럼 사용하기 위해서 활용하는 개념이라고 보시면 됩니다.

저는 간단하게 사각형을 예시로 들었습니다. 단면계수는 간단하게 단면 2차 모멘트에 최외곽 반지름( 혹은 높이)을 나누어주면 구할 수 있습니다.
극관성모멘트
극관성모멘트는 단면을 수직 좌표계에서 보고 계산한 것이 아닌 극 좌표계로 보고 계산한 단면 2차 모멘트라고 보시면 됩니다. 단면이 y축에 x만큼, x축에 y만큼 떨어져 있을 때의 모멘트가 아니라 그냥 단순히 해당 단면이 원점으로부터 얼마만큼 떨어져있을 때 계산한 단면 2차 모멘트라는 뜻입니다.

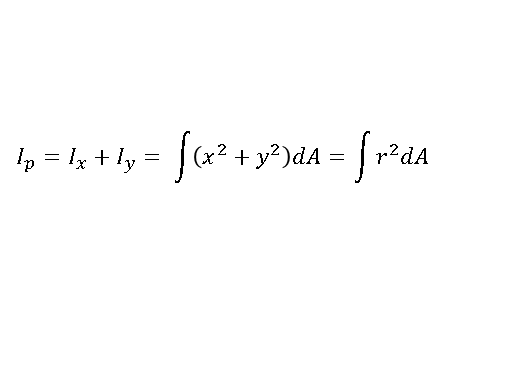
사각형을 단순하게 직교 좌표계에서 본 것이 아니라 극좌표계 형식을 적용하여 계산한 것이기 때문에 x축에 관한 단면 2차 모멘트와 y축에 대한 단면 2차 모멘트의 합으로 나온 것입니다.
아마도 극 관성모멘트를 어떻게 써야할 지 헷갈리시는 분들이 많을 것 같네요. 간단하게 정리하자면 극 관성 모멘트는 토크와 전단응력, 비틀림 응력을 계산하실때 적용하면 됩니다. 극좌표계가 회전을 설명할 때 쓰는 좌표계고, 비틀림또한 단면이 회전하는 형태의 변형이기 때문에 그냥 단면 2차 모멘트가 아닌 극 관성모멘트를 적용하게 되는 것입니다.
반면 굽힘도 회전이긴 하지만 단면이 회전하는게 아니기 때문에 극 관성모멘트가 아니라 그냥 단면 2차 모멘트를 적용해서 재료역학 문제를 해결합니다.
반응형
'기계공학- 일반기계기사 > 정역학 및 재료역학' 카테고리의 다른 글
| Beam ( 보 ) 의 해결법 - 정정보, 단순보, 간단한 하중일 경우 접근법 (0) | 2021.12.12 |
|---|---|
| 일반기계기사 - 트러스 구조물이 나올 경우 (간단한 문제의 경우) (0) | 2021.03.06 |
| 일반기계기사, 재료역학, 단면 2차 모멘트에 대한 이야기 (0) | 2021.02.27 |
| 일반 기계기사 - 단면 1차 모멘트 (0) | 2021.02.19 |
| KOCW 강의 추천 - 재료역학 (0) | 2021.02.15 |