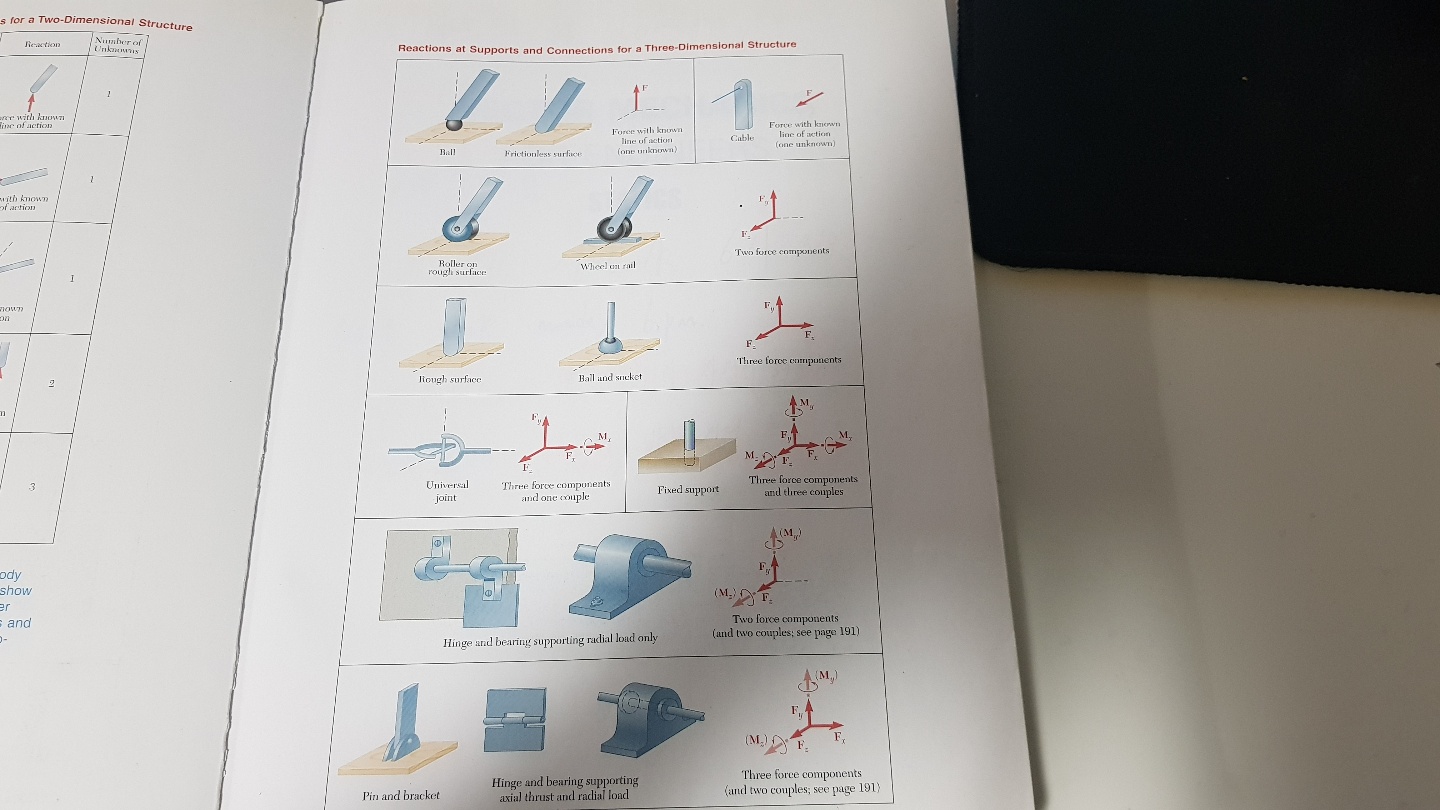
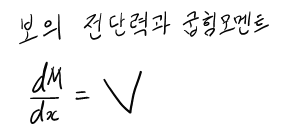반응형
안녕하세요! 공돌이 인생무상입니다!
정역학 이야기를 너무 오랬동안 안했네요 허허허...이번에는 드디어! 정역학 이야기를 좀 해보려고 합니다. 저는 역학을 너무 좋아하기에... 이번 포스팅은 행복하게 해보겠습니다!
참고자료
본문의 문제는 VECTOR MECHANICS FOR ENGINEERS STATICS 10th 의 연습문제 7.29번을 참고하여 풀이 만들었습니다.

문제에 대한 풀이
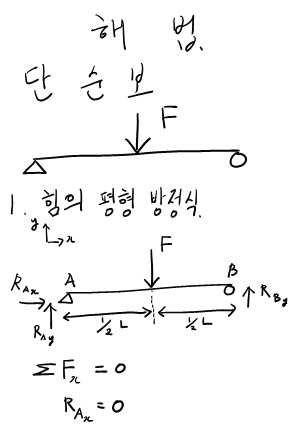
참고 자료의 7.29에 대한 내용을 그림으로 나타내면 아래와 같습니다.

우선 좌표 방향을 설정해줍시다. 저는 늘 위쪽방향을 +y, 오른쪽 방향을 +x 로 둡니다. 이렇게 하는게 습관이 되어서 그렇게 문제를 푼답니다.

단위 하중 문제는 단위 하중을 하중으로 변경해야합니다. 정역학에서 나오는 단위 하중은 단위 길이당 하중의 크기를 나타내는데요. 단위 하중은 길이를 곱하면 하중으로 변환할 수 있습니다. 이 상황에서는 우선 하중만 필요하니까 P=wL로 표기한 후 하중의 위치는 L/2 로 두었습니다. 하중의 위치 정하는 것은 이전에 언급했던 도심 개념을 이해하면 바로 하중의 위치를 정할 수 있습니다. 이 문제에서는 하중이 일정한... 사각형 형상인데 사각형의 도심은 중심부에 위치하므로 L의 중심부인 L/2에 두었습니다. 이 다음 문제인 7.30에서는 삼각형으로 단위하중이 표기되는데 그런 경우에는 하중의 위치를 삼각형의 도심에 두면 됩니다. 다음 포스팅에서 자세히 언급하도록 하겠습니다.
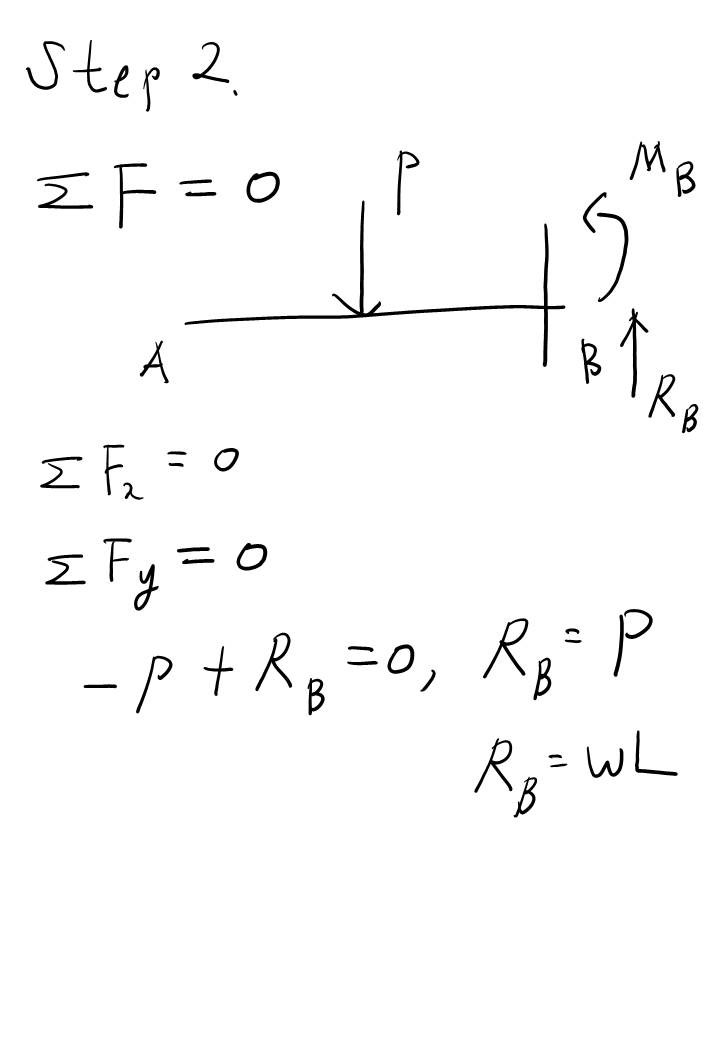
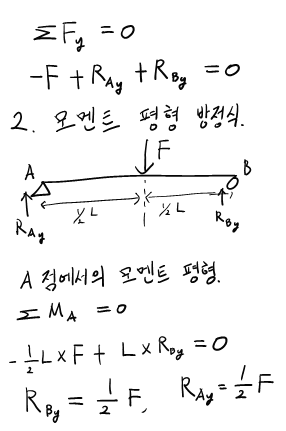
Step 2는 B 지점의 반력을 구하는 과정입니다. 이건 쉽죠?
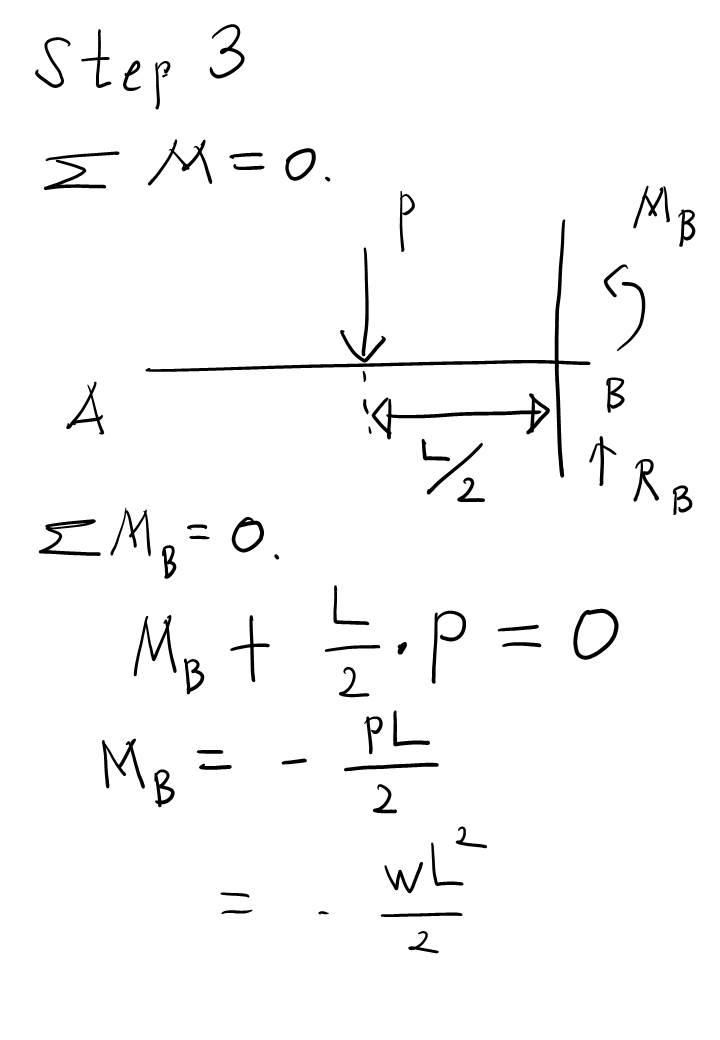
Step 3는 B 지점의 모멘트를 구하는 것입니다. 이것도 쉽지요?
Step 4 부터는 S.F.D를 그려봅시다. S.F.D는 Shear Force Diagram이라해서 전단력 선도라고 하는 것입니다. 이 그림을 그리는 능력... 별거 아닌거 같지만 나중에 꼭 필요한 것이니까 여기서 확실히 마스터해봅시다!
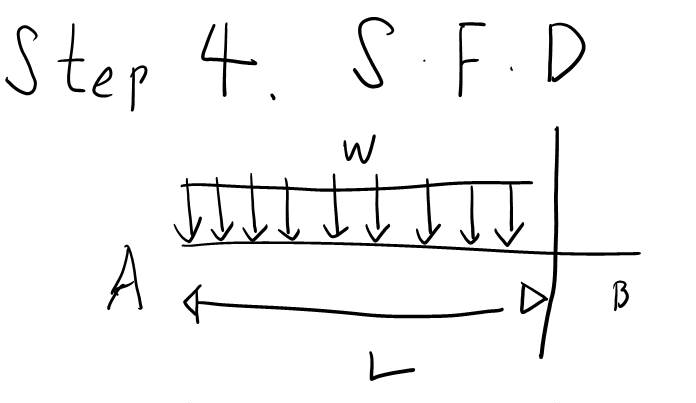
저는 S.F.D의 시작점을 A점으로 정했습니다. 시작점을 어디다 정하는지는 본인이 맘대로 정하시면 됩니다. 단, 부호가 달라질 수 있으니까..부호 잘 설정해야합니다. 부호는 풀다보면 헷갈려서 잘 틀리니까요.
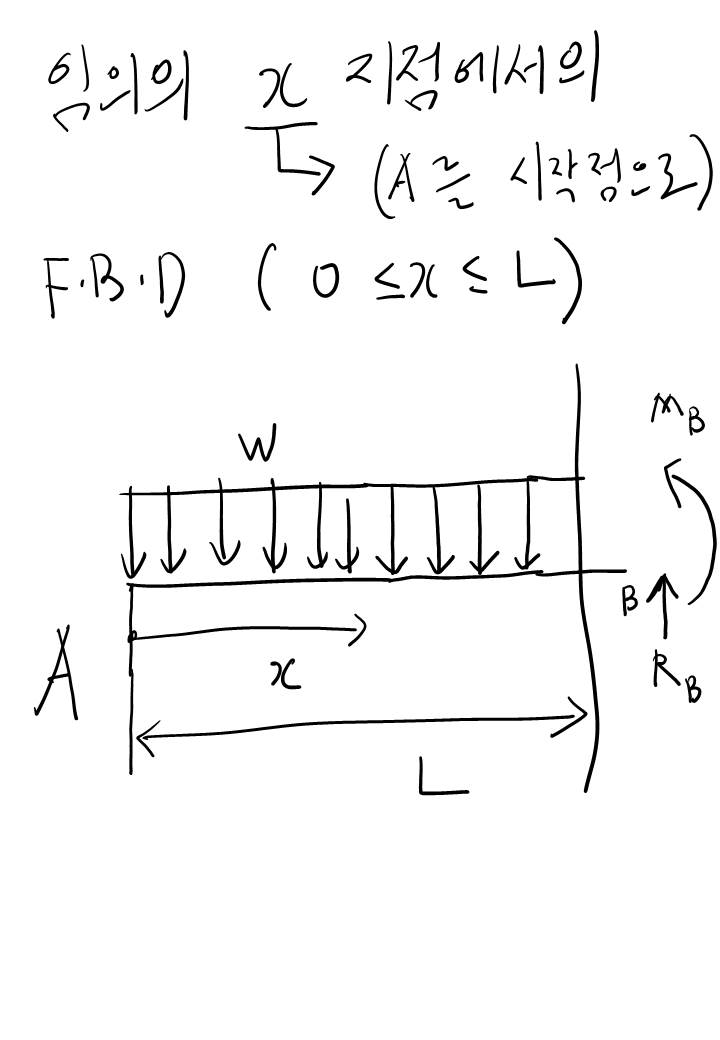
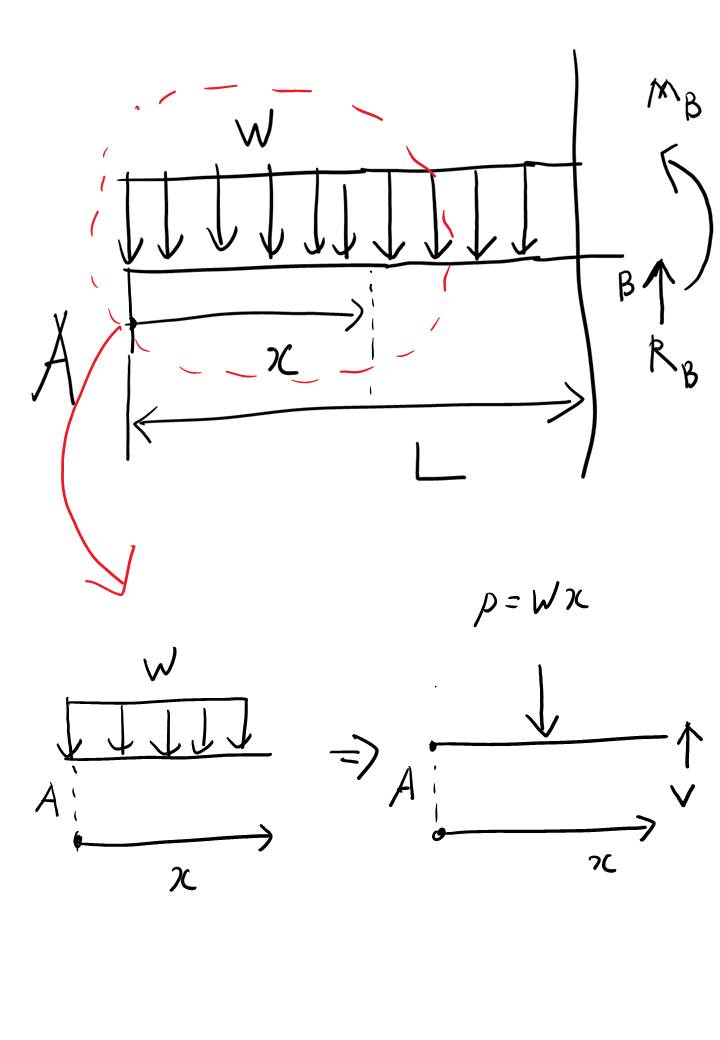
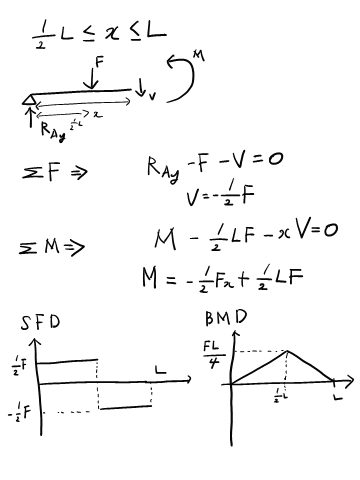
이건 임의의 X 지점에서 V(전단력)의 함수를 구하는 과정입니다. 임의의 x 길이에서 하중은 wx로 표현이되며 이 하중과 V라는 하중의 식을 통해 전단력의 함수를 구할 수 있습니다. 아래 그림처럼요.
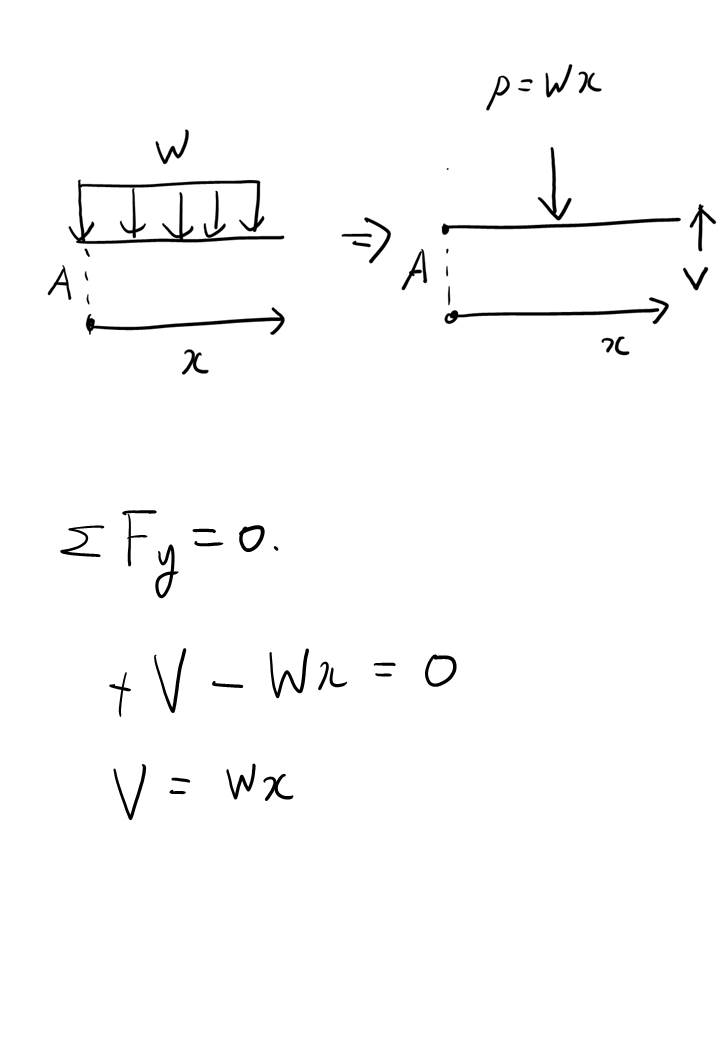
이렇게 함수가 구해지면 그림은 바로 그려낼 수 있습니다.
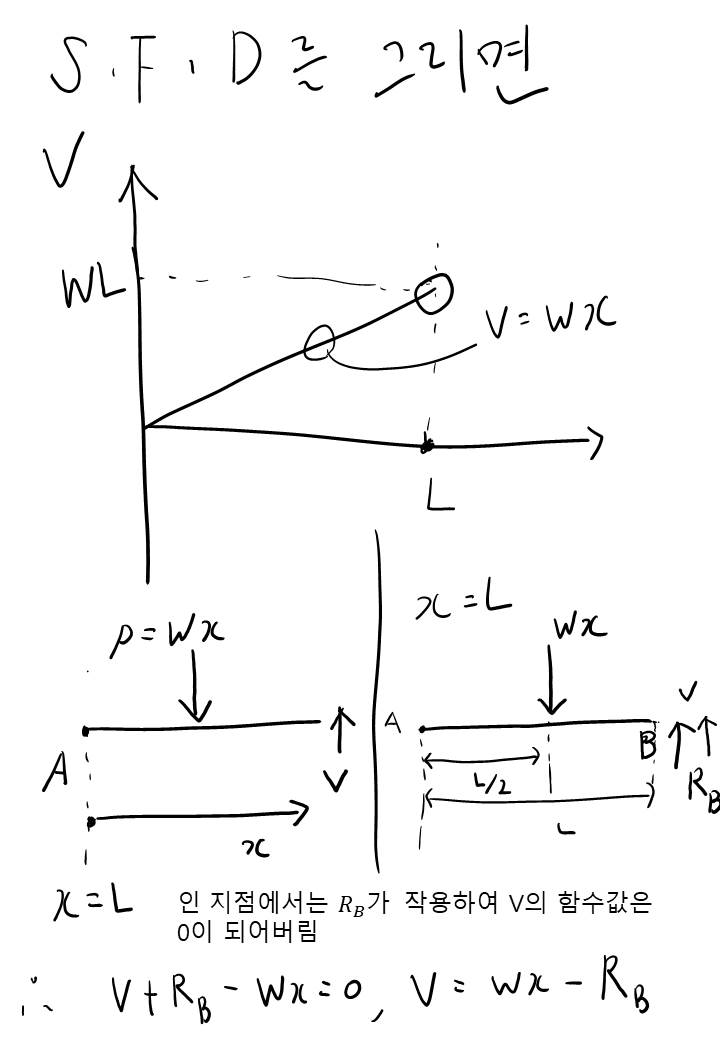
여기서 주의할 것은 A 점을 시작으로 함수를 그렸지만, x가 L인 지점에서는 반력이 적용됩니다. 반력이 작용해야 전체 보에서 하중은 0이 되며 이를 수식으로 표현한 것입니다. 그리고 위 그림에서 x=L인 지점의 함수값을 불연속값으로 만들었는데 이렇게 해야 x=L인 지점에서 0이 된다는 것을 표현하려고 한 것입니다. 고등학생 시절 배운 불연속 개념을 여기 적용했습니다.
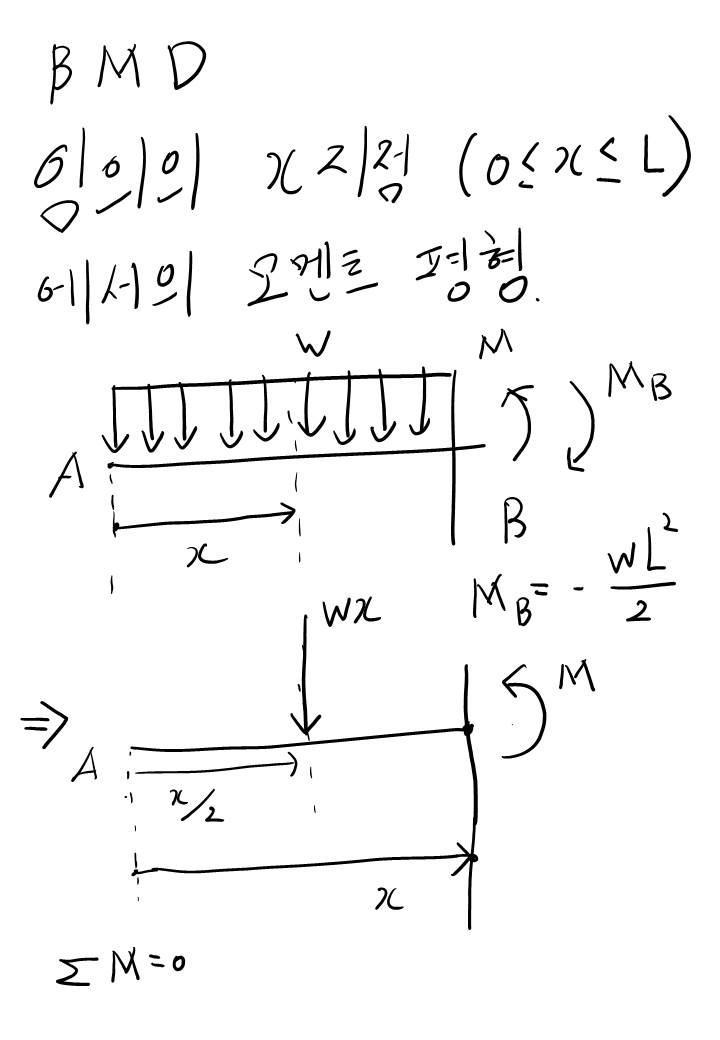
B.M.D (Bending Moment Diagram)도 S.F.D와 같은 방식으로 해결하면 됩니다.
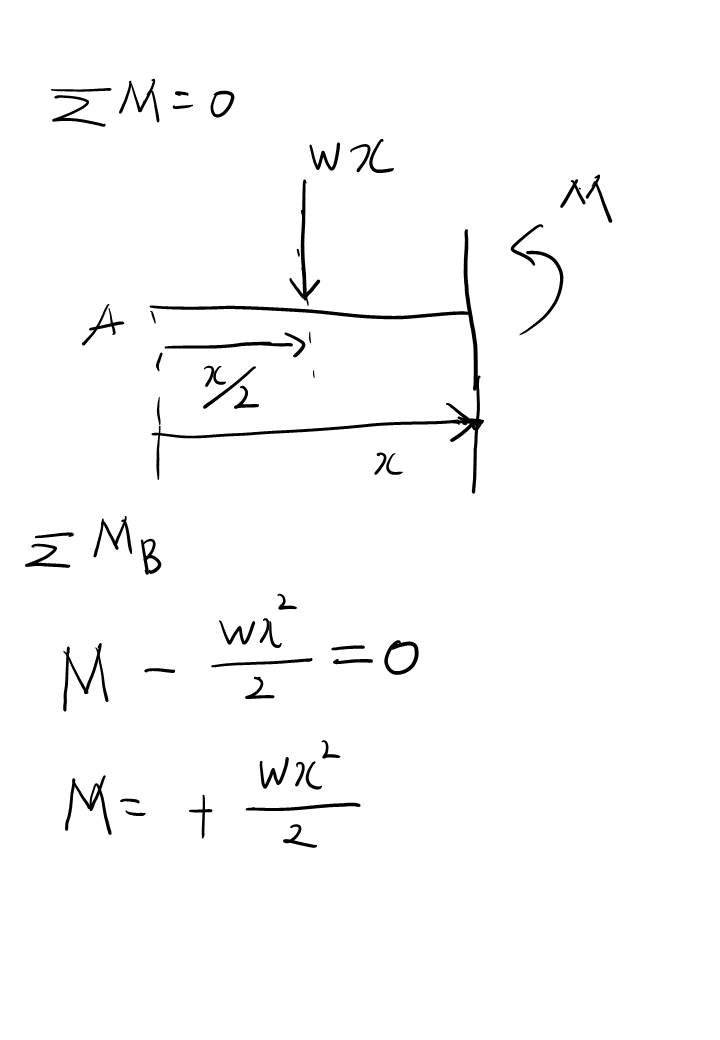
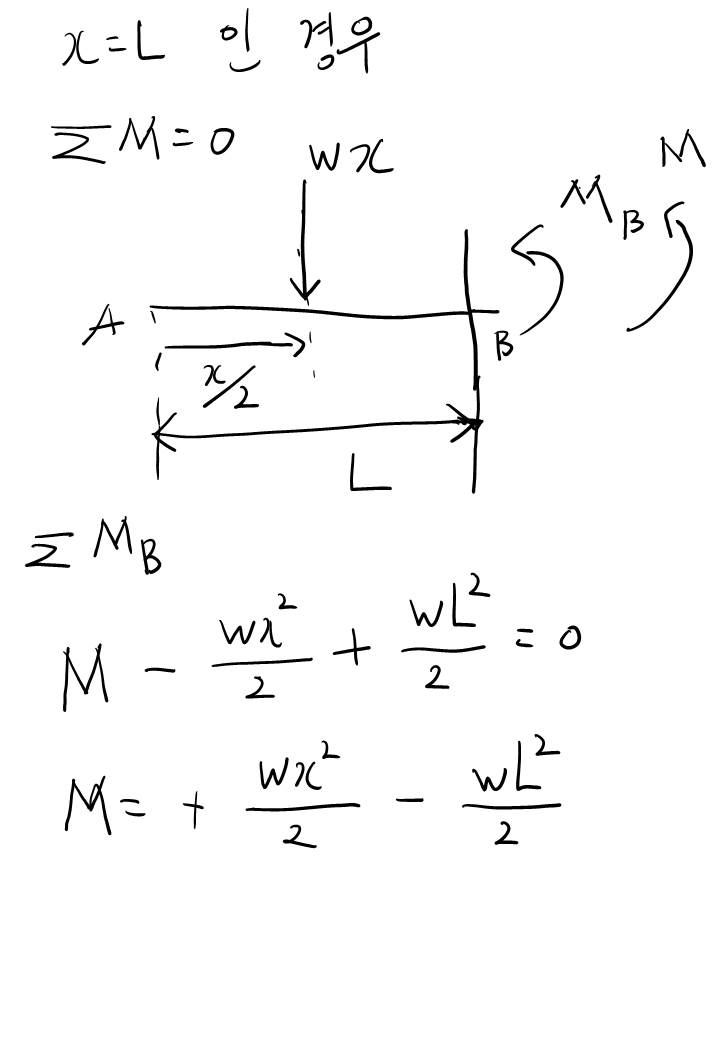
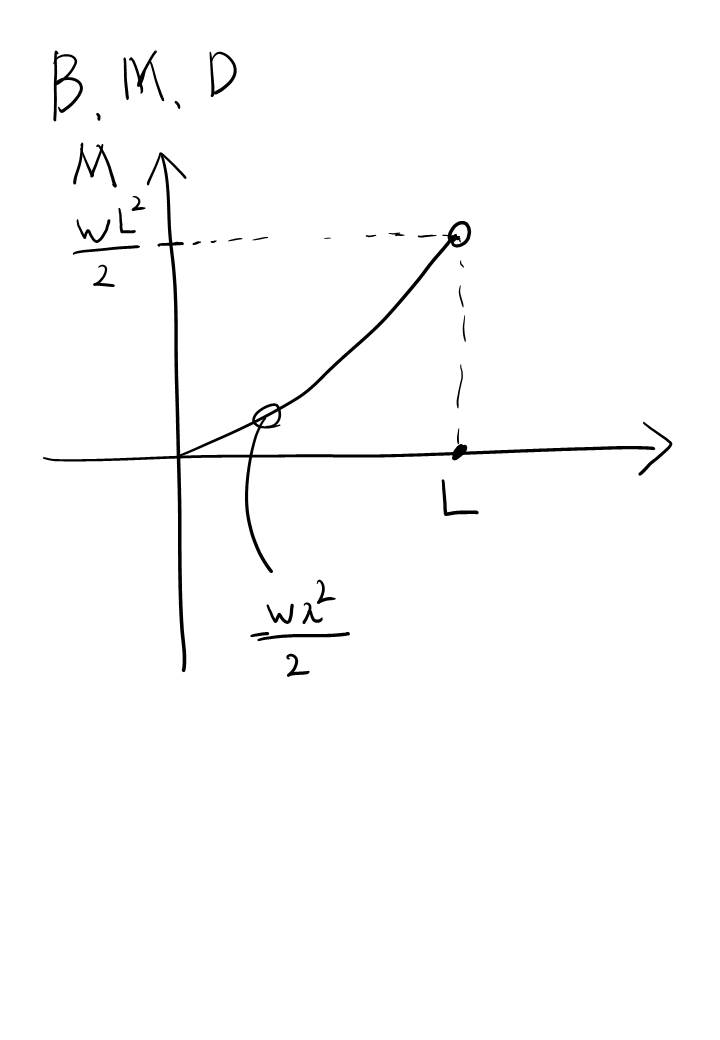
굽힘 모멘트 역시 x=L인 지점에서 반력으로 작용하는게 있기 때문에 빼줘야합니다. 그래야 x=L, 즉 B 지점에서의 모멘트 역시나 0이 되니까요.
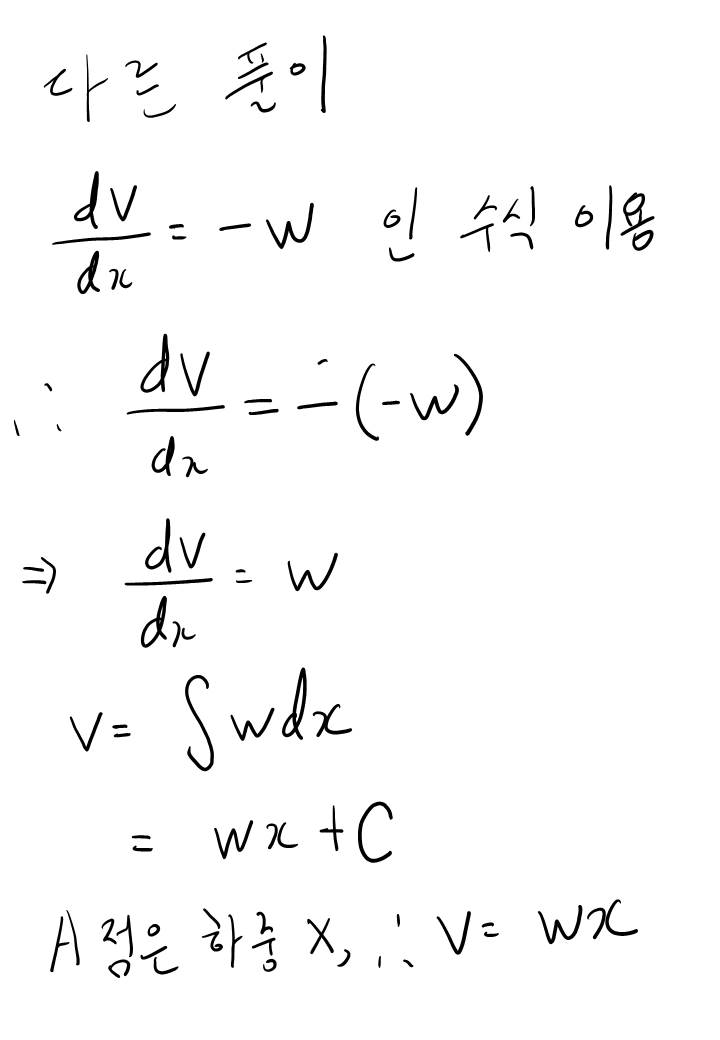
이 풀이는 단위하중과 하중간의 관계식을 이용해 문제를 해결하는 방법입니다. 눈치가 빠르신 분들은 단위 하중이 왠지 하중과 어떤 수식 관계에 있을 것이라는 생각을 하셨을 텐데... 맞습니다. 이 내용은 참고자료로 쓴 책의 373 페이지에도 자세히 나와있습니다.
이 수식을 한 번 자세히 보도록 할까요?
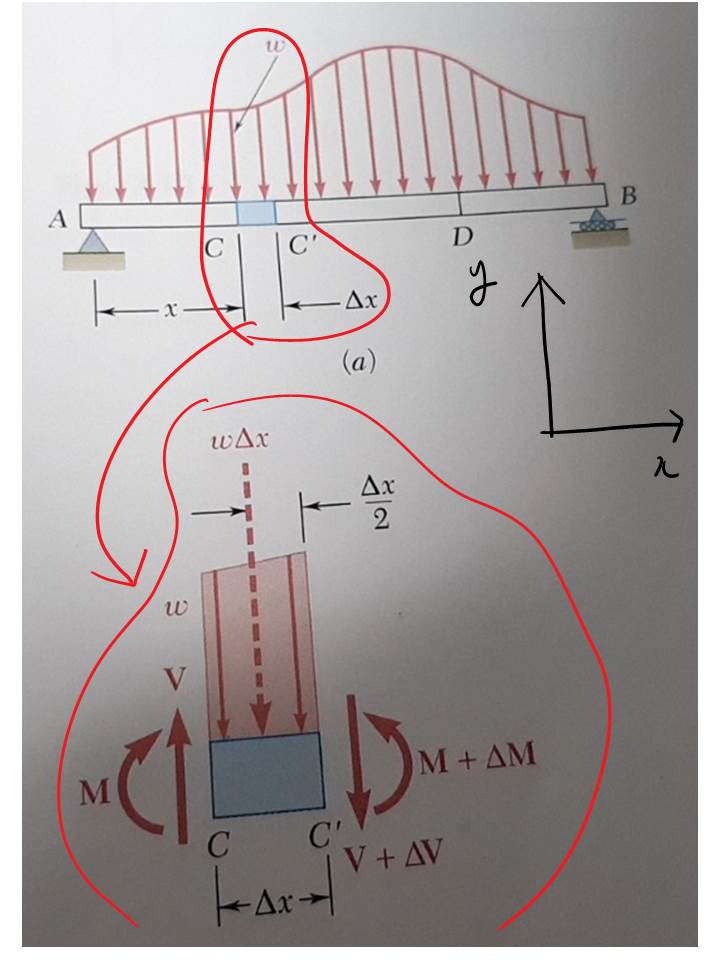
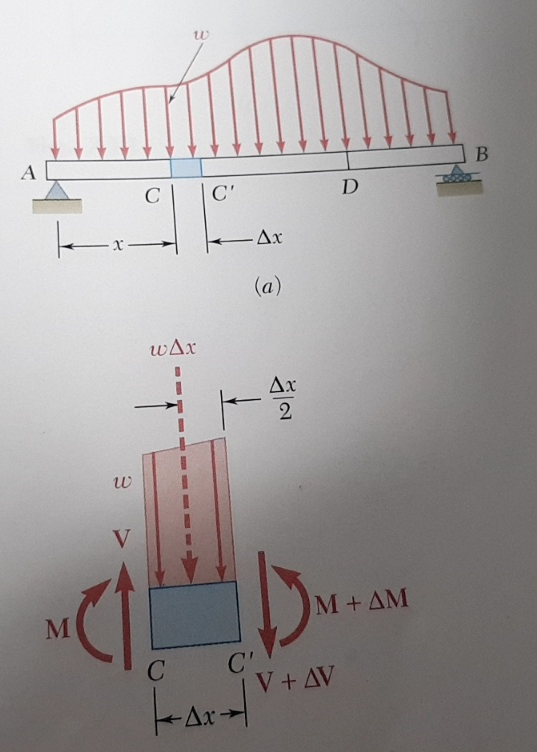
C점과 C' 지점은 아주 미세한 간격을 가진 지점으로 가정한 것입니다. 이 상태에서 두 지점들의 힘과 모멘트의 수식을 정리하면 아래그림과 같습니다.
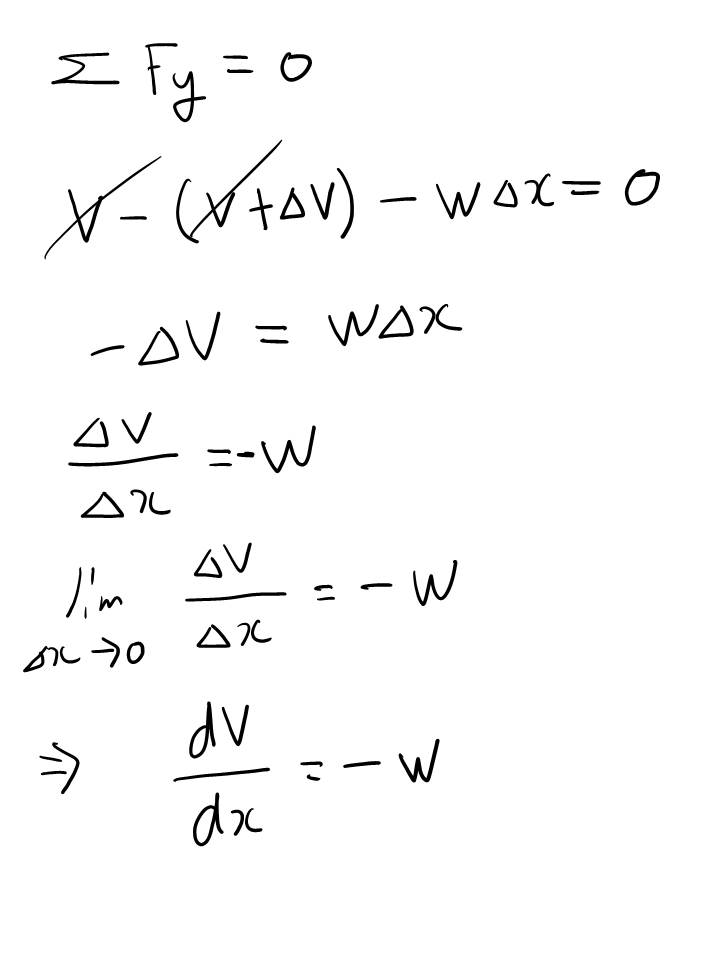
위의 V와 w 간의 내용은 이해하는데 어려움이 없을 거라 생각합니다. 하지만...
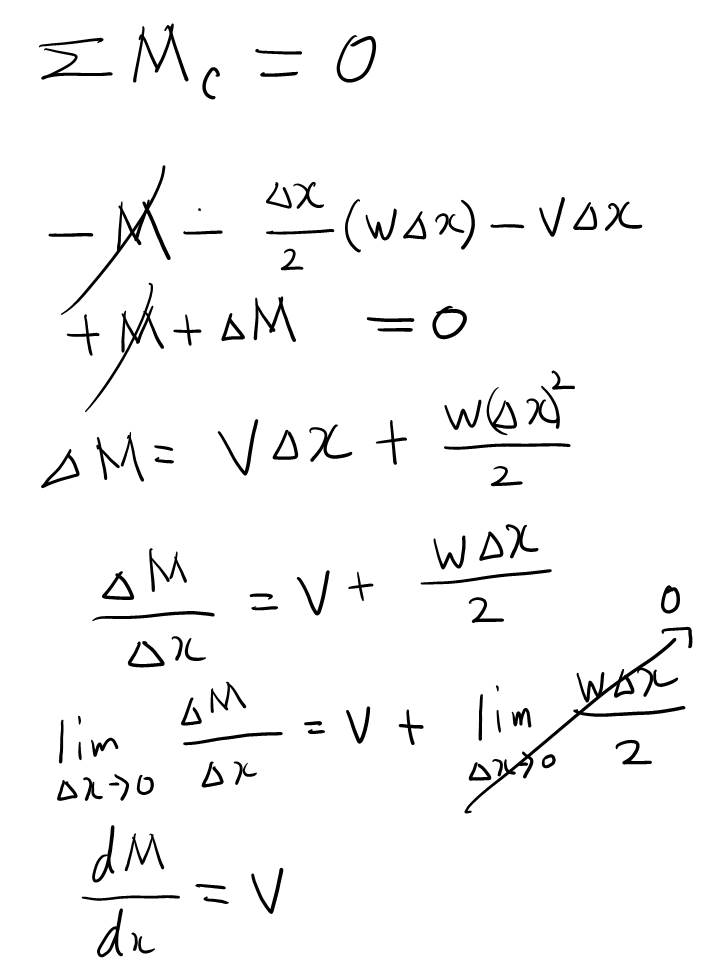
여기는 좀 어려울 수도 있는데.. 요약하면 w는 같이 곱해진 △x 가 0이 되어버리는 바람에 소거되어서 결국 V와 M만 남는 관계식이 되는 것이지요.
즉, 이 두 관계식 V와 w의 관계, 그리고 M과 V의 관계식이 이렇게 증명되며 두 개의 관계식을 잘 이용하면 보 (Beam)문제를 적분을 이용해 쉽게 해결할 수 있다는게 요지입니다. 같은 원리로 모멘트도 적분을 이용하면 쉽게 구할 수 있습니다.
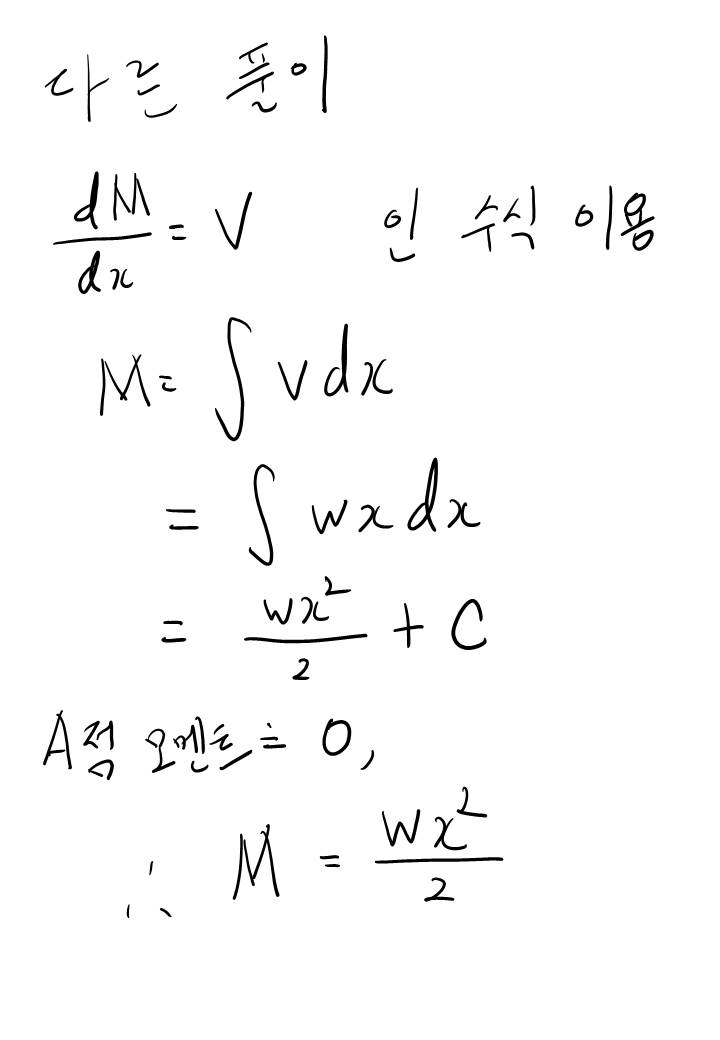
적분을 이용해 V, M의 함수를 구하고 x=L 지점에서 반력과 반력모멘트의 영향을 고려해 선도를 그리면 문제는 쉽게 해결할 수 있습니다. 이제 다음 번 포스팅은 단위하중이 간단한 형상이 아니라 복잡한 삼각형 형상일 경우 어떻게 해결해야할 지 한 번 도전해봐야겠네요!
반응형
'기계공학- 일반기계기사 > 정역학 및 재료역학' 카테고리의 다른 글
| [정역학] Beam(보)문제 해결편 - 단순보의 집중 하중 에 대한 대응법 (3) | 2024.06.08 |
|---|---|
| [정역학] Beam(보)문제 해결편 - 정정보의 어려운 단위 하중(삼각형) 에 대한 대응법 (0) | 2024.06.07 |
| Beam ( 보 ) 의 해결법 - 정정보, 단순보, 간단한 하중일 경우 접근법 (0) | 2021.12.12 |
| 일반기계기사 - 트러스 구조물이 나올 경우 (간단한 문제의 경우) (0) | 2021.03.06 |
| 단면 2차 모멘트에서 파생된 계산법들을 재밌게 풀어보자 (1) | 2021.03.01 |