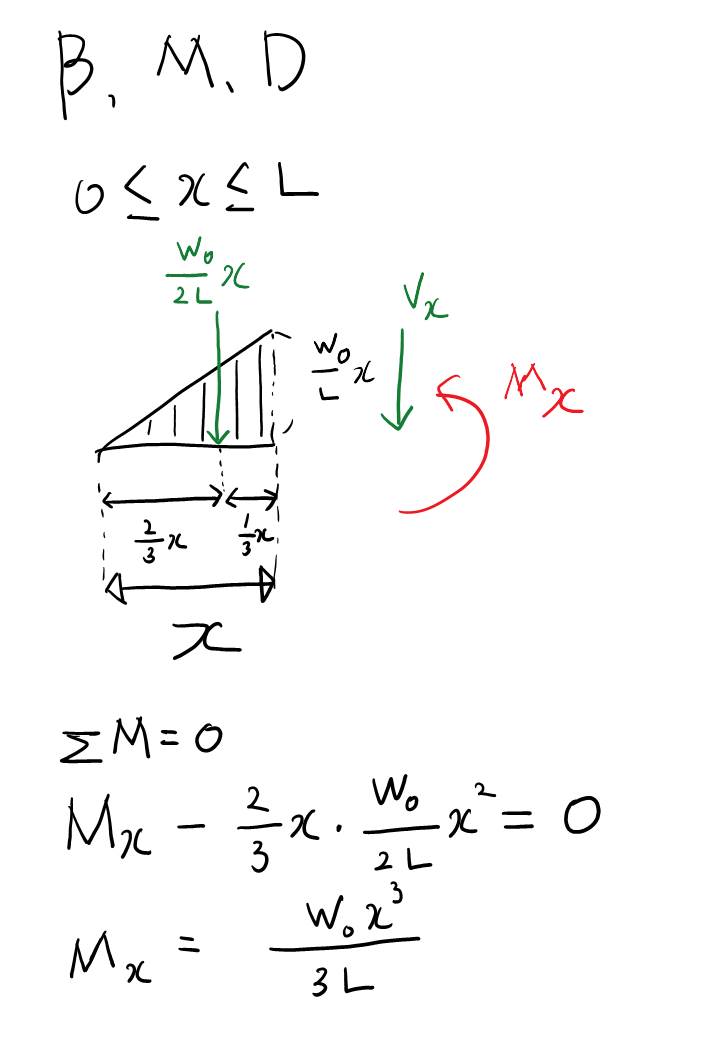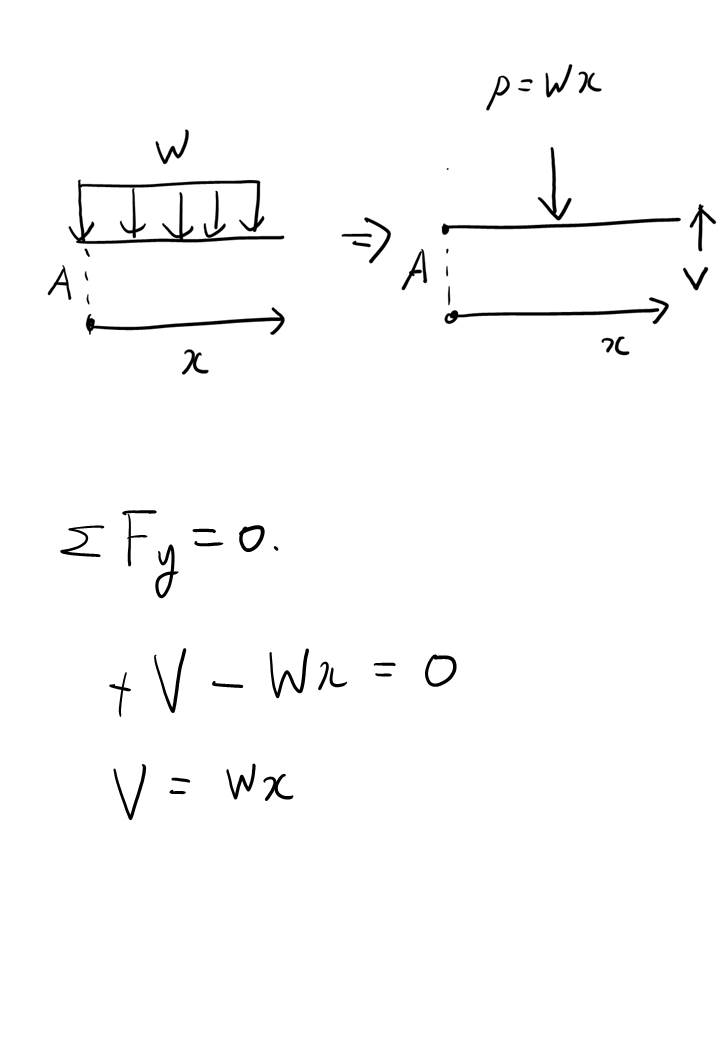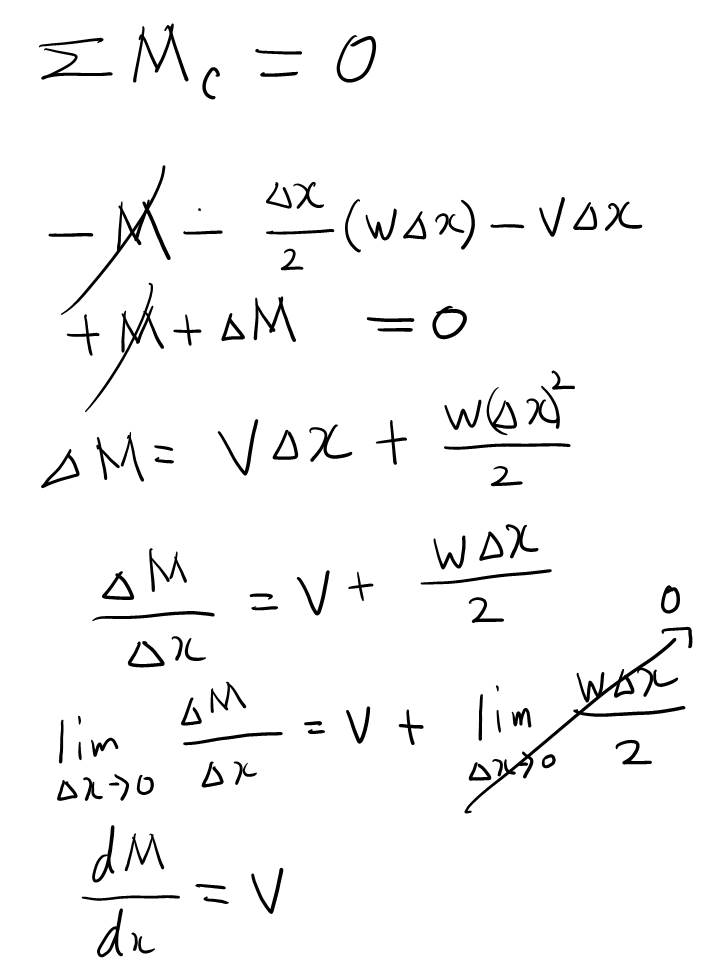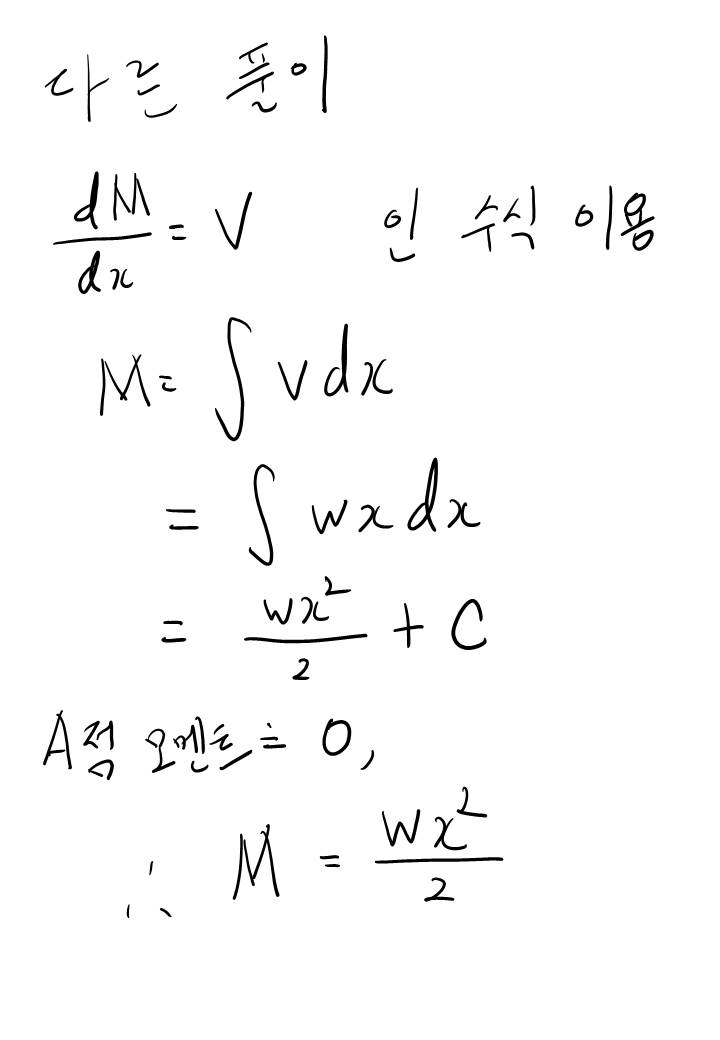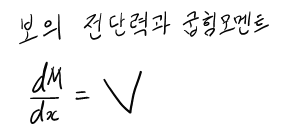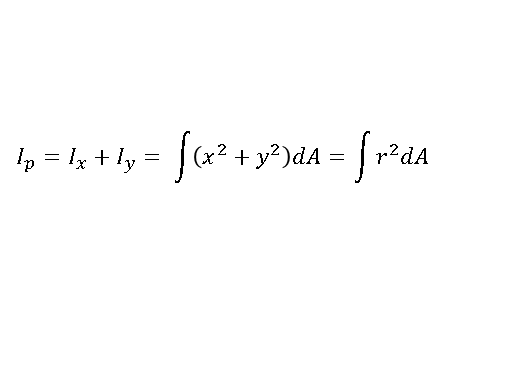반응형

안녕하세요! 공돌이 인생무상입니다!
기계공학 하면서 가장 먼저접하는 정역학... 그 중에서 오래봐야하고 또 재료역학에도 영향을 미치는
보(BEAM)에 관한 해석법을 계속 업로드하고 있습니다. 이번에는 외팔보가 아닌 단순보로 갖고 왔고요.
단순보에서 많이 보이는 문제 유형인...
여러개의 집중하중이 있다면 어떻게 풀어나갈것인가 알아보도록 하겠습니다!
풀이법
문제는 그렇게 어렵지 않습니다. 어렵지 않은데... 좀 번거로워요. 문제 역시 제 정역학 교재였던..
BEER 외 2명, VECTOR MECHANICS FOR ENGINEER STATICS에서 가지고 왔습니다. 연습문제 7.36번입니다.

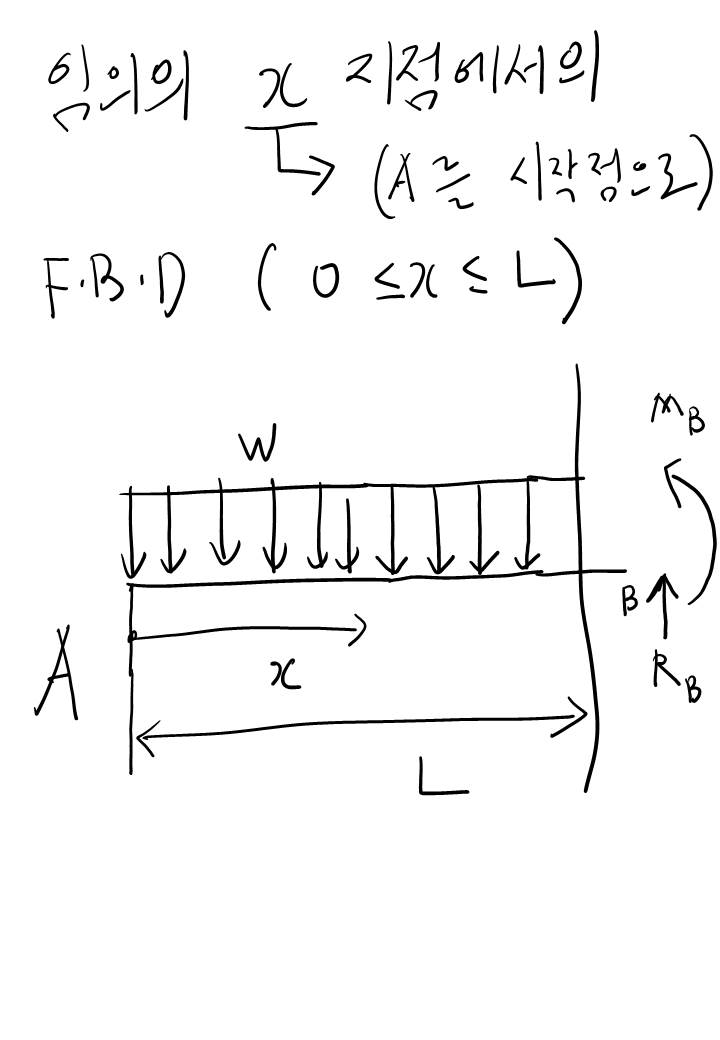
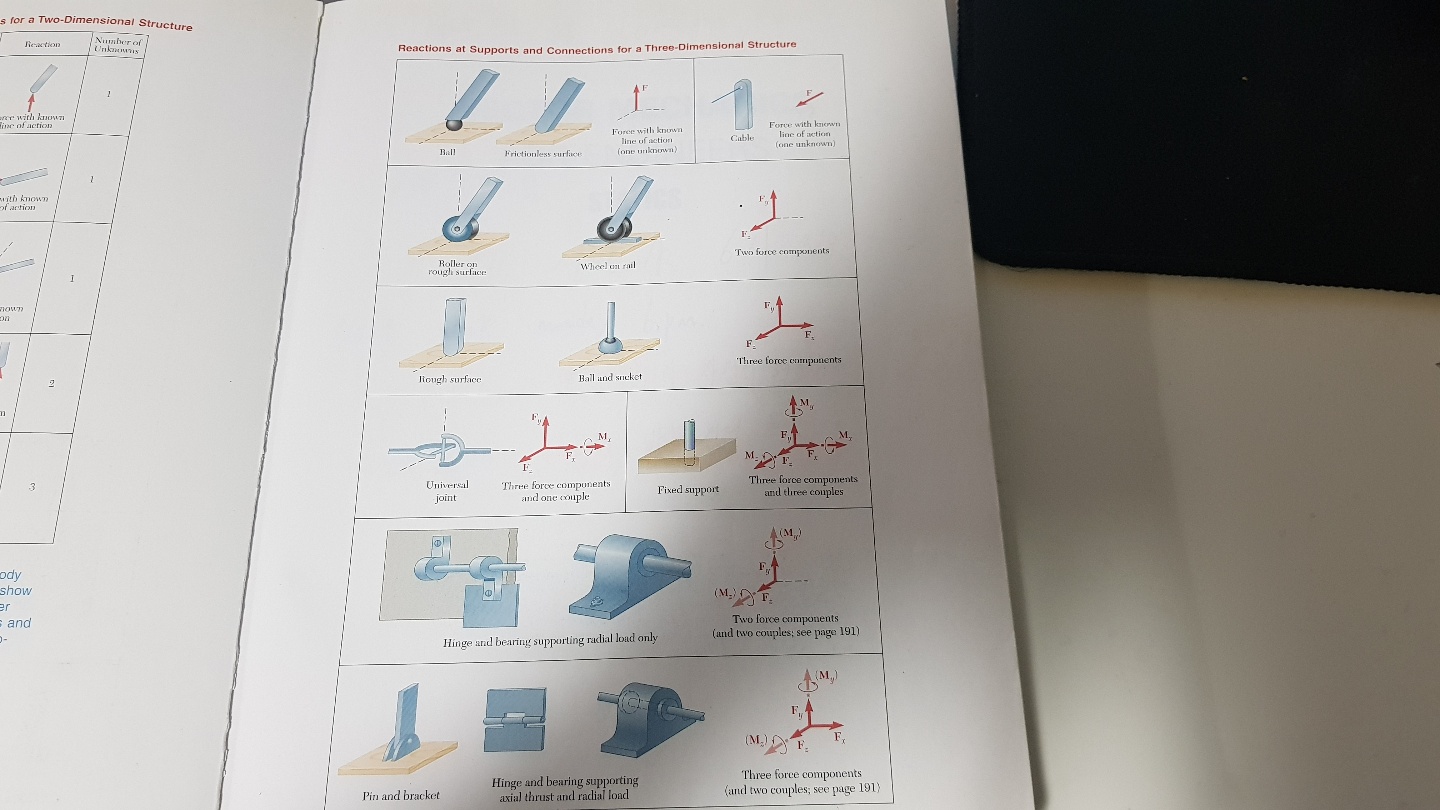
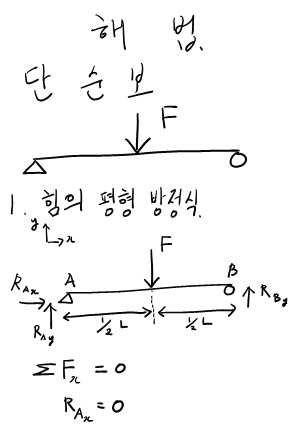
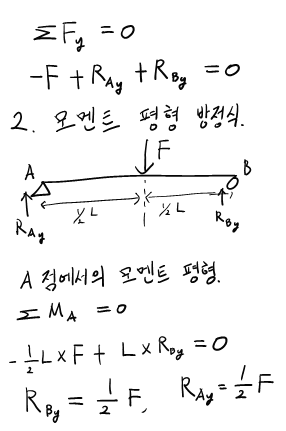
문제 설명을 잠시 하자면.. A점과 B점은 모두 모멘트 반력은 없는 지지점입니다. 정역학 책에 지지대와 반력에 대해서 설명한 도표들이 있을테니 거기를 참고하시면 더 자세한 설명을 볼 수 있을 겁니다. 추후에 다시 다뤄봐야겠네용...ㅎㅎ

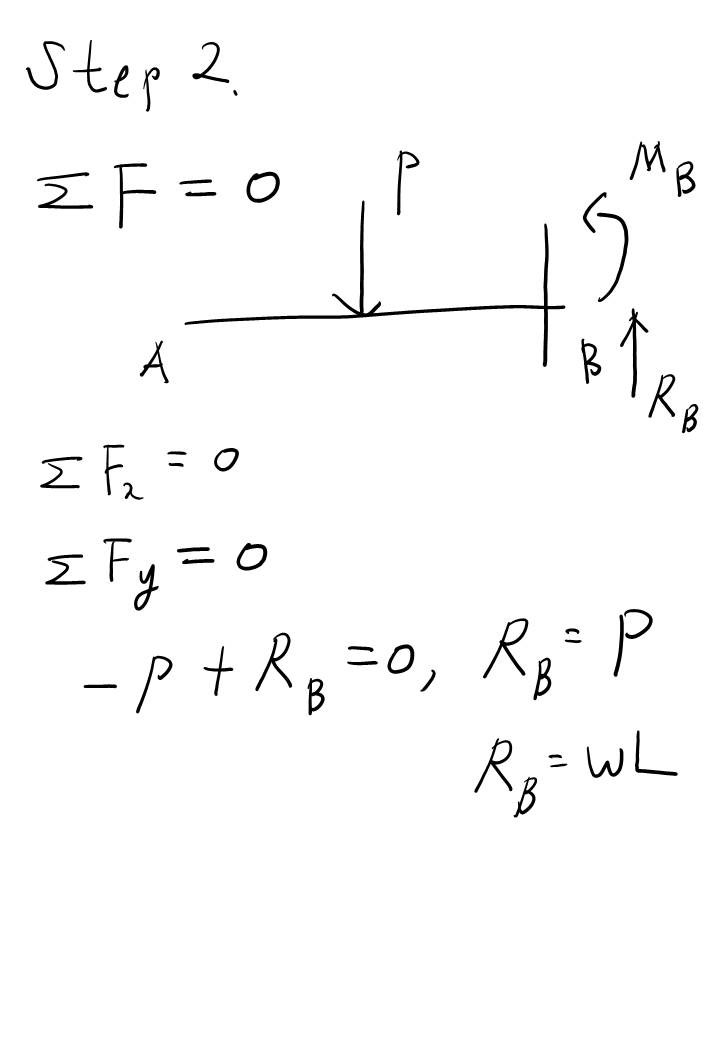
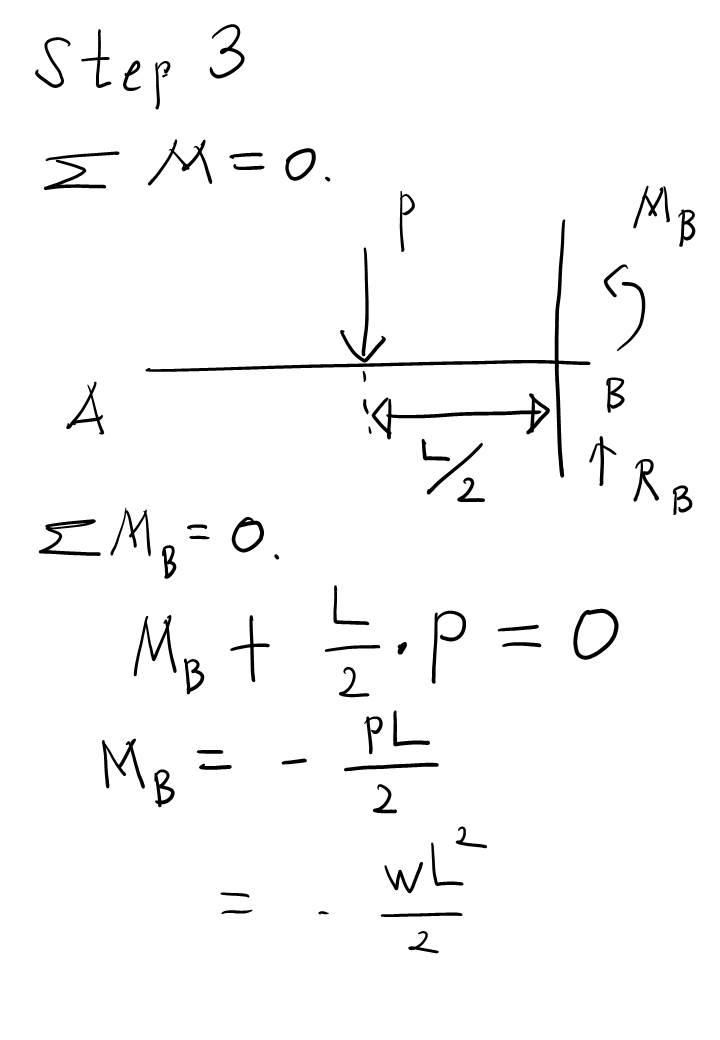
여기까지 해서 A, B 점의 반력을 구했습니다. 반력을 구하는데 총 두 개의 방정식을 사용하였네요. 첫 번째는 힘의 평형 방정식을 이용했고, 두 번째는 모멘트 평형 방정식을 이용했습니다. 미지수가 두 개 (Ra, Rb) 였고 방정식도 두 개였으니 풀릴 수 있었네요.
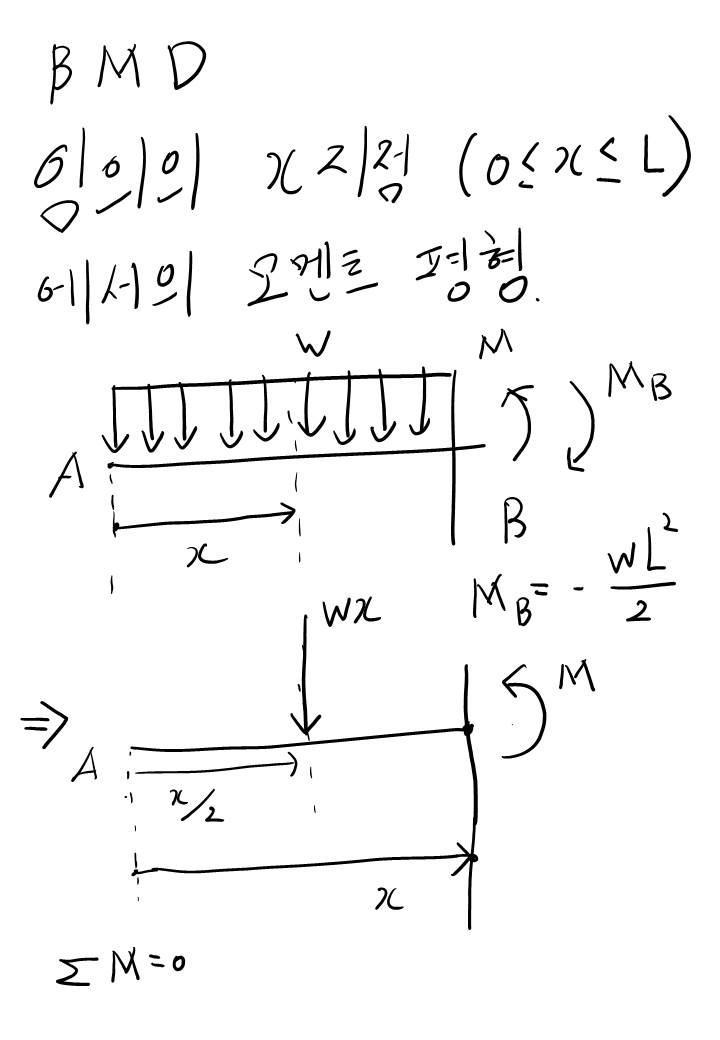
보 문제는 이것만 기억하세요. 첫 번째는 F.B.D (Free Body Diagram)을 그리고!
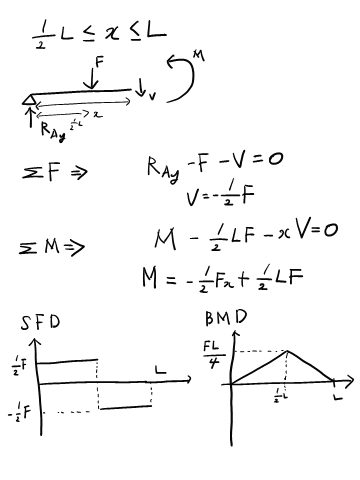
두 번째! 힘과 모멘트 평형 방정식을 푼다. 그러면 반력을 구할 수 있고 S.F.D, B.M.D를 그려낼 수 있을 겁니다!
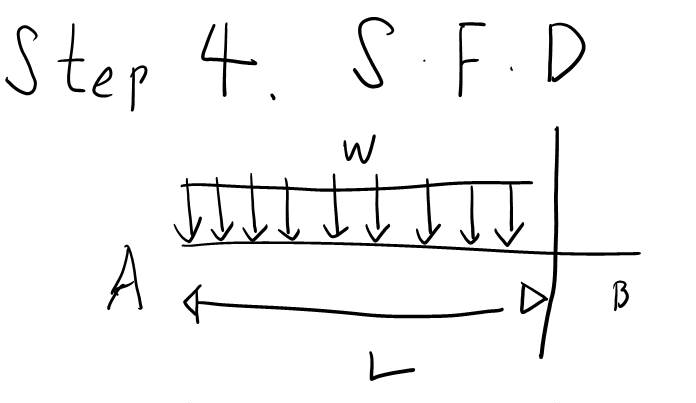
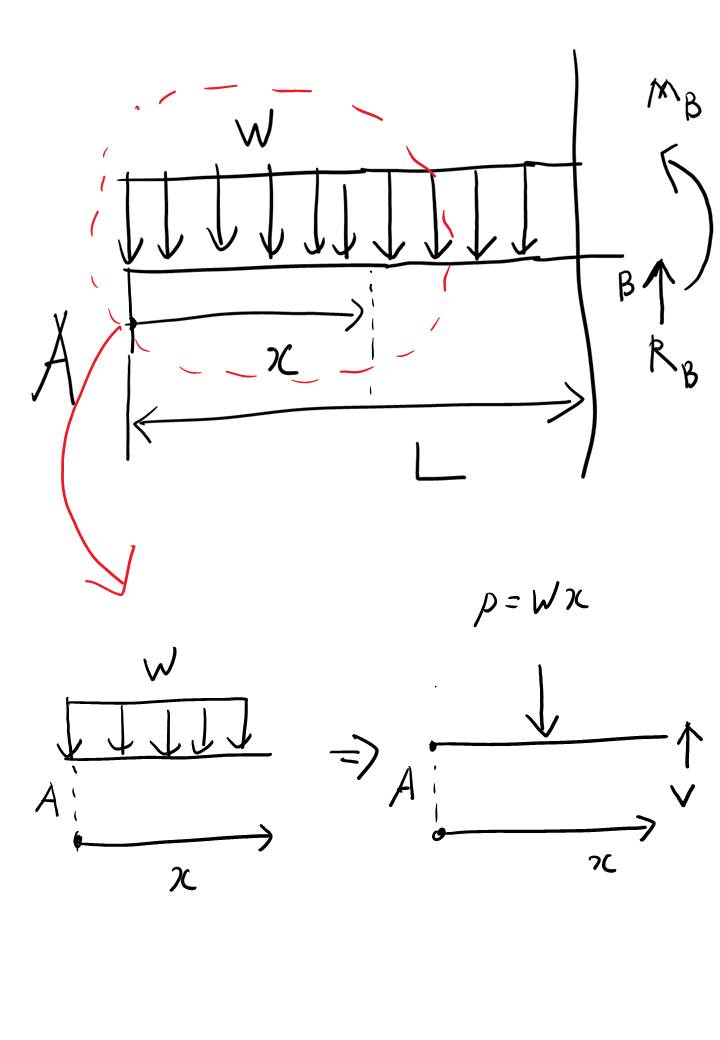
하지만 이 유형은 S.F.D랑 B.M.D 그려내는게 많이 귀찮고 번거롭습니다. 왜냐면... 집중 하중이 3개나 되다보니 이 하중 구간별로 나눠야하는데 그 구간이 무려 4개나 됩니다. 또한... B.M.D 그릴때도 똑같이 4개 구간으로 나뉘게되니 한 번에 처리해봅시다.
왜 구간별로 나뉘어야하냐면 하중이 어느 지점에서 갑자기 툭 툭 내려가다가 반력이 마지막에 작용해서 보의 하중이 0이되는... 불연속적인 조건이기 때문에 그렇습니다.
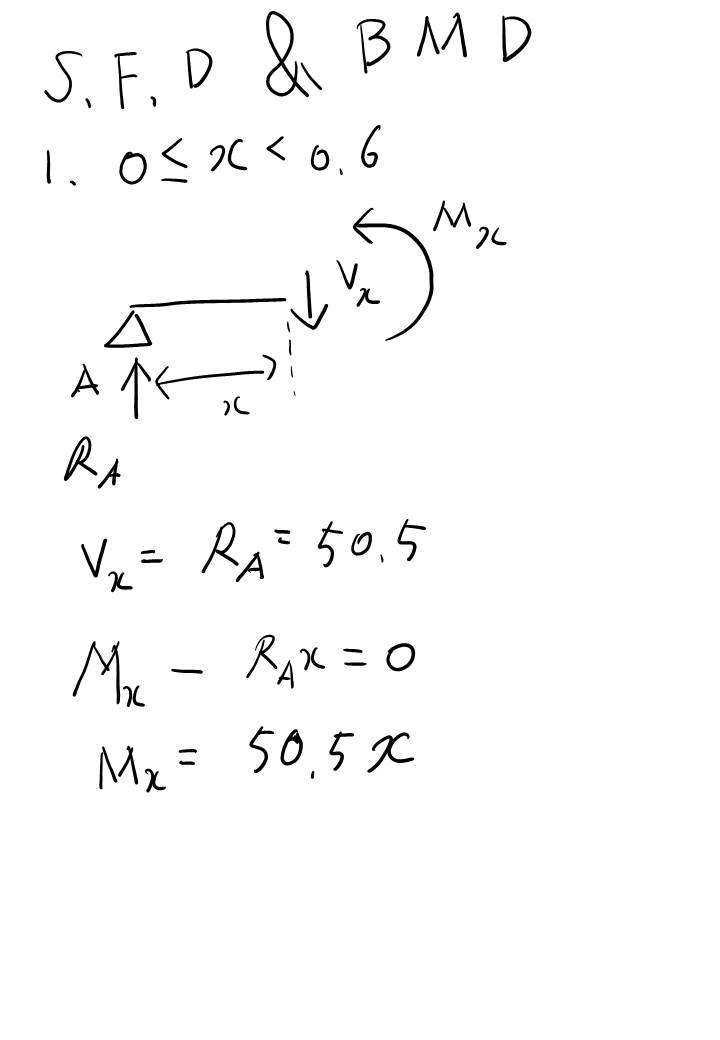
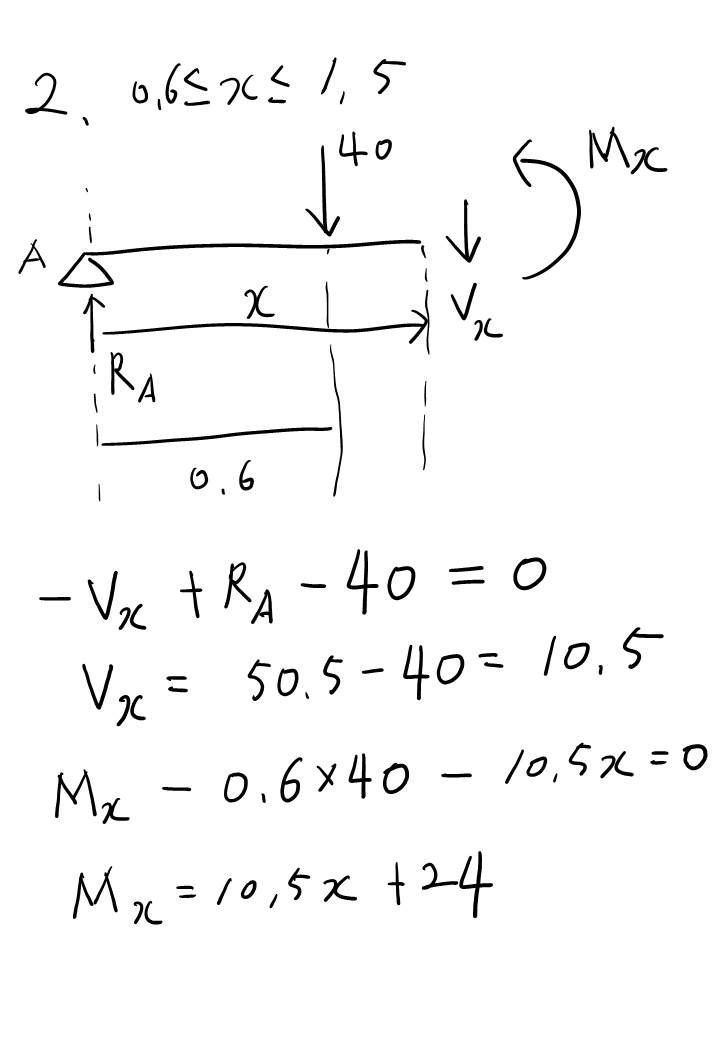
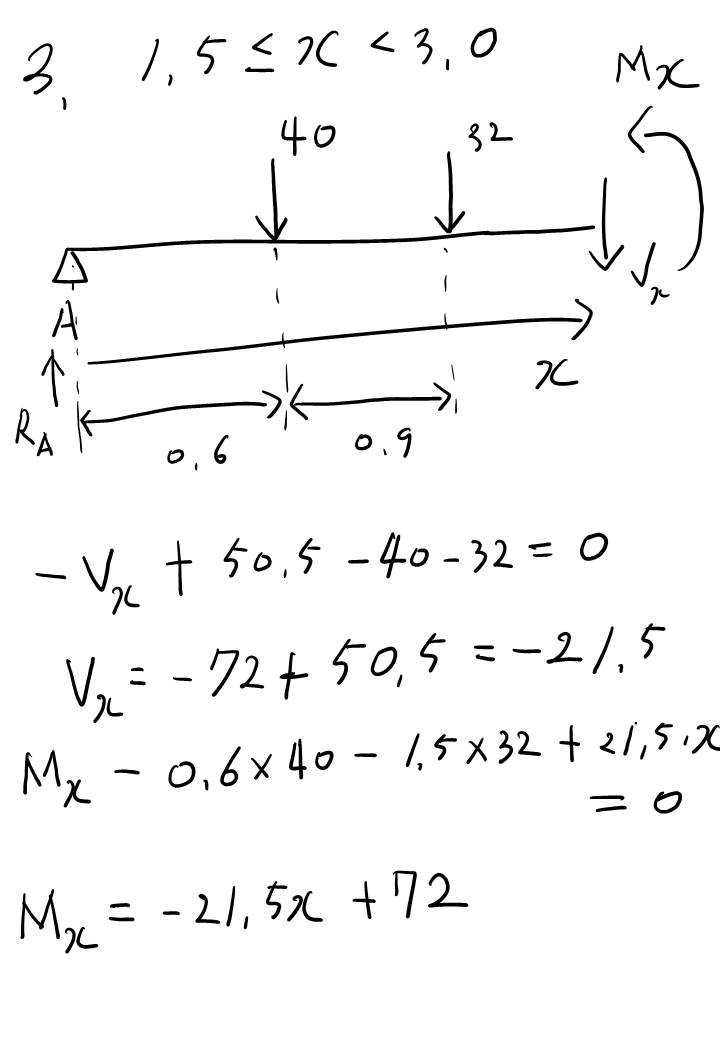
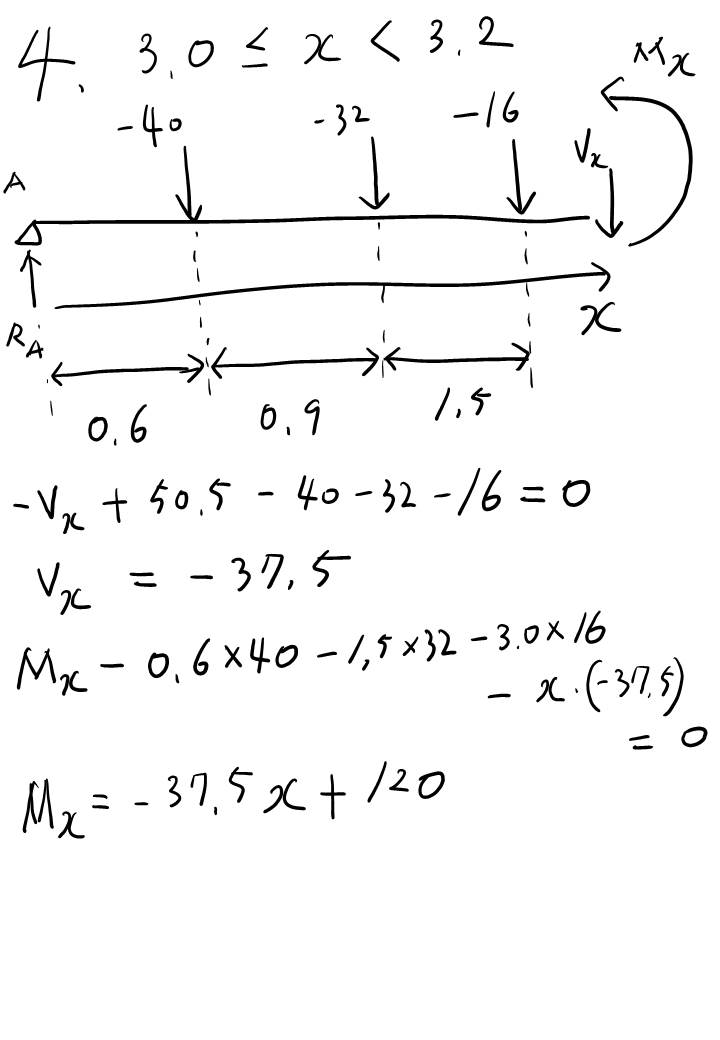
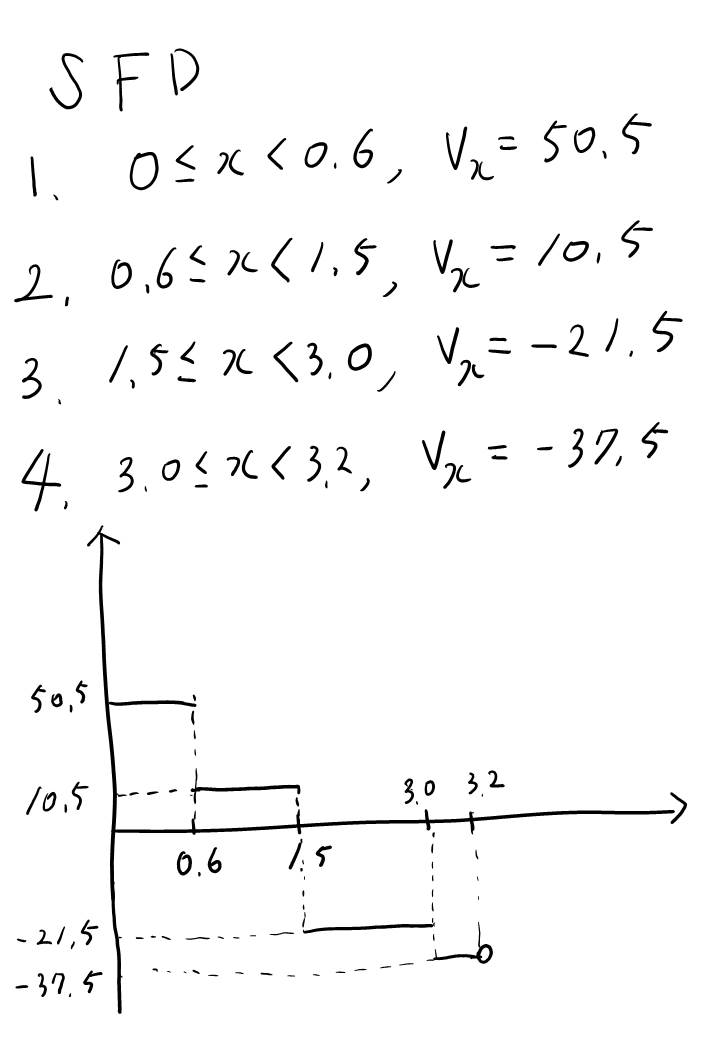
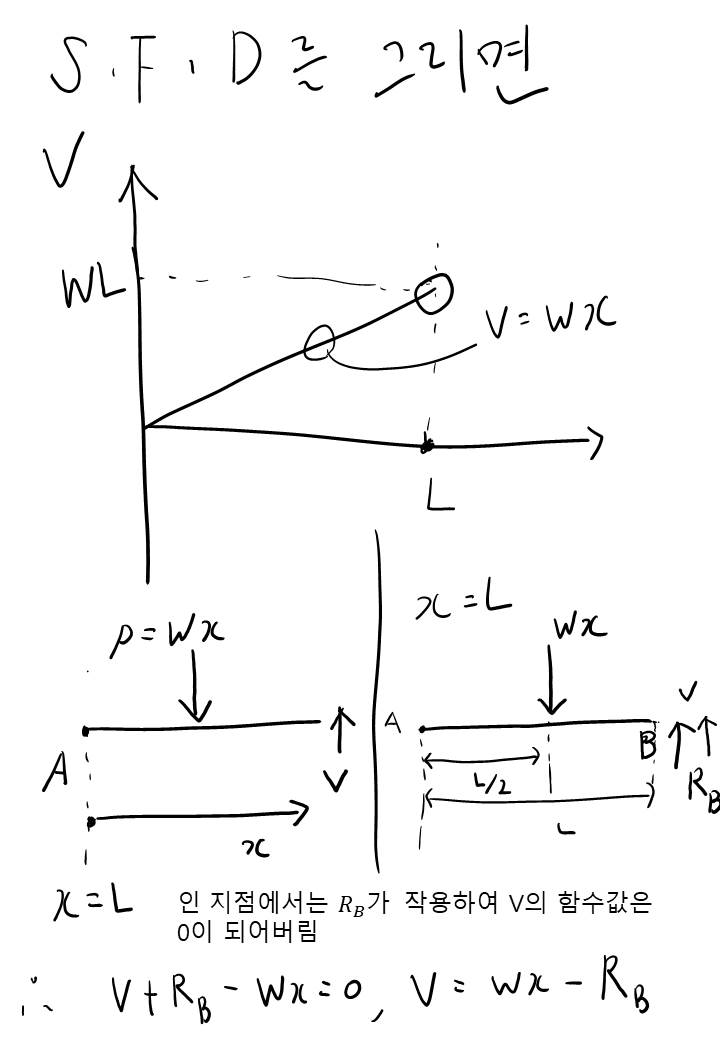
이런 유형은 S.F.D, B.M.D 그리기가 귀찮을 겁니다. 하중이 세 개나 있다보니 구간 별로 나눠야하고..
구간이 네 개나 되다보니 엄청 ... 어려운건 아닌데 번거롭다는 느낌이 드는 문제 유형입니다.
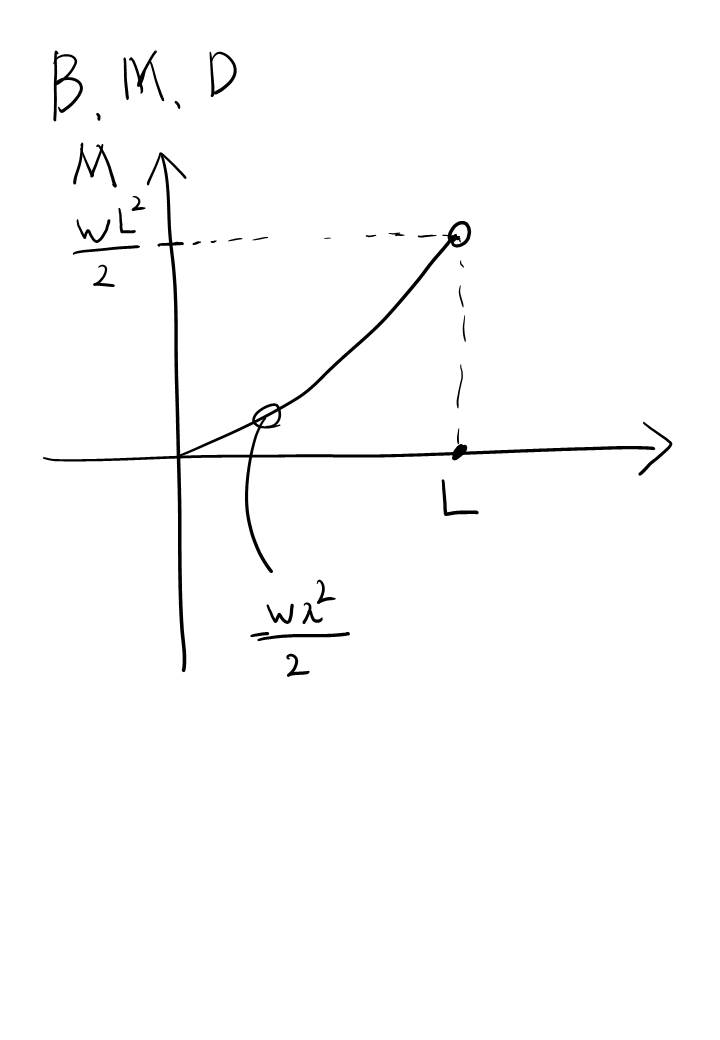
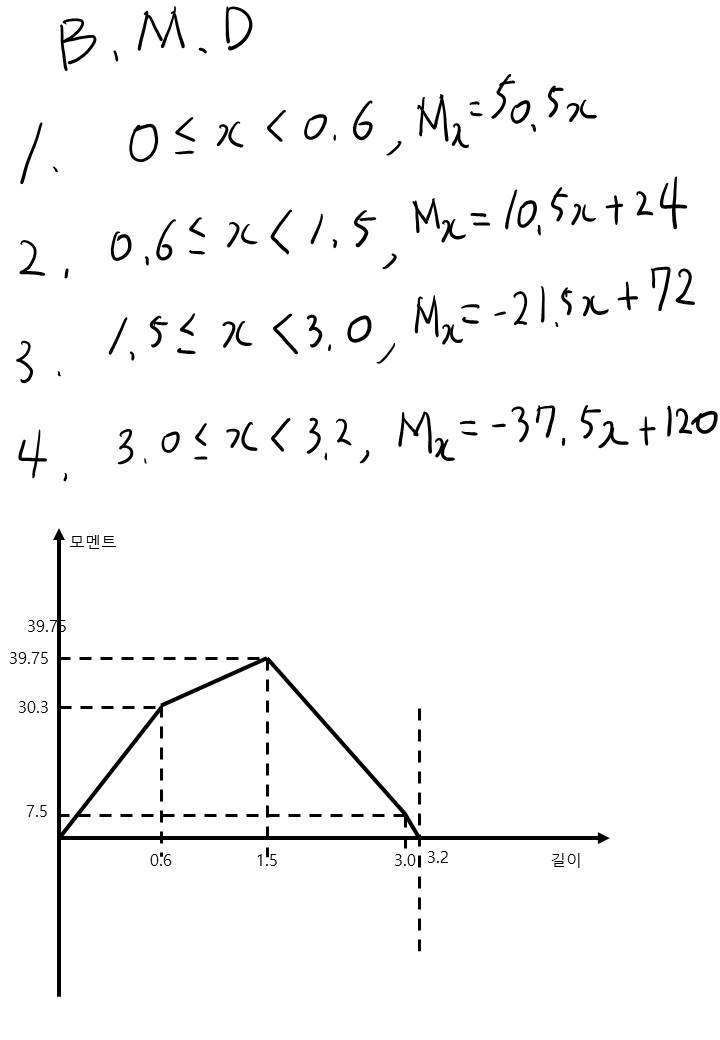
구간이 나눠지다보니 이 문제 유형에서는 모멘트 선도(B.M.D)가 불연속은 아니지만, 전단력선도(S.F.D)는 불연속적인 모양이 되네요. 번거롭고 불연속적이긴 하지만 검산을 하면 틀렸는지 맞았는지 바로 알 수 있지요.
절대로 어려운 유형은 아니기 때문에 이 정도 레벨은... 잘 마무리해서 좋은 점수를 받아야겠지요?
반응형
'기계공학- 일반기계기사 > 정역학 및 재료역학' 카테고리의 다른 글
| [정역학] Beam(보)문제 해결편 - 정정보의 어려운 단위 하중(삼각형) 에 대한 대응법 (0) | 2024.06.07 |
|---|---|
| [정역학] Beam(보)문제 해결편 - 정정보의 간단한 단위 하중 에 대한 대응법 (0) | 2024.04.13 |
| Beam ( 보 ) 의 해결법 - 정정보, 단순보, 간단한 하중일 경우 접근법 (0) | 2021.12.12 |
| 일반기계기사 - 트러스 구조물이 나올 경우 (간단한 문제의 경우) (0) | 2021.03.06 |
| 단면 2차 모멘트에서 파생된 계산법들을 재밌게 풀어보자 (1) | 2021.03.01 |